7 - Coordinate systems and map projections
Explain the relevance of reference surfaces, coordinate systems, and coordi-nate transformations in mapping (level 1 and 2).
Concepts
-
Coordinate system
Different kind of coordinates are used to position objects in a two- or three-dimensional space.
Spatial coordinates (also known as global coordinates) are used to locate objects either on the earth’s surface in a 3D space, or on the earth’s reference surface (ellipsoid or sphere) in a 2D space. Specific examples are the geographic coordinates in a 2D or 3D space and the geocentric coordinates, also known as 3D Cartesian coordinates.
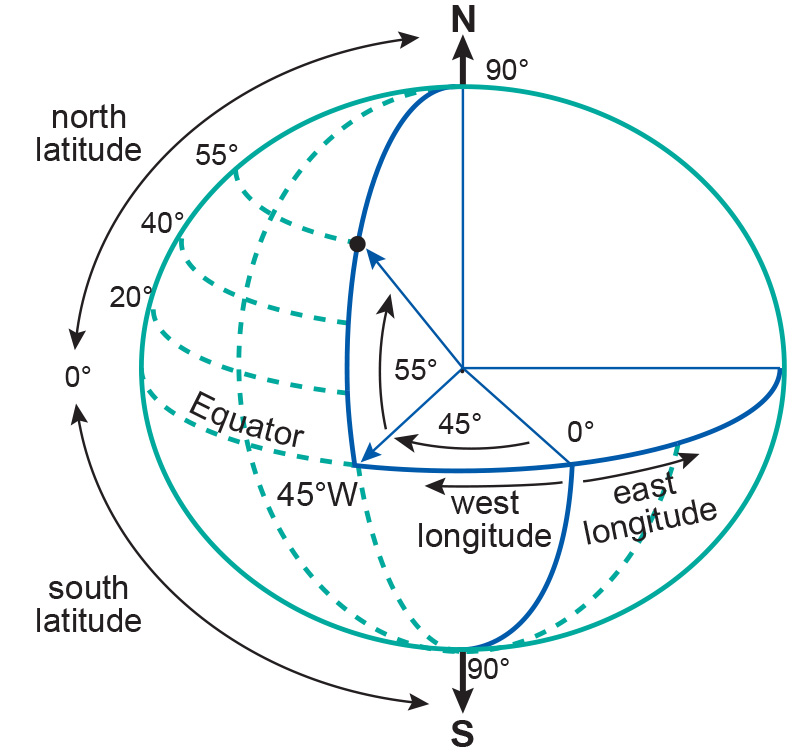
The latitude and longitude angles represent the 2D geographic coordinate system. Planar coordinates on the other hand are used to locate objects on the flat surface of the map in a 2D space. Examples are the 2D Cartesian coordinates and the 2D polar coordinates.
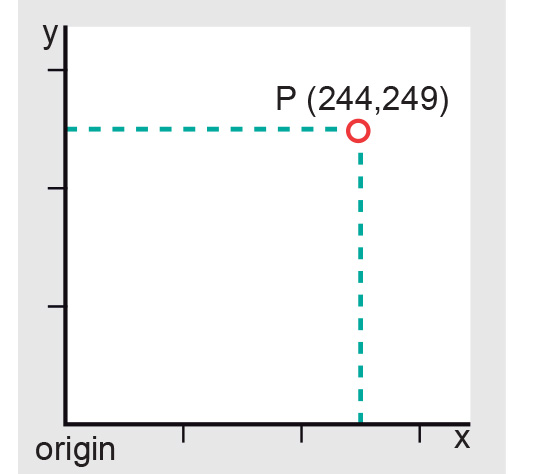
An illustration of the 2D Cartesian coordinate system -
Ellipsoid
The most convenient geometric reference surface for mapping purposes is the oblate ellipsoid (Figure 1). It provides a relatively simple figure of the Earth which fits the geoid to a first order approximation. An ellipsoid is formed when an ellipse is rotated about its minor axis. This ellipse which defines an ellipsoid or spheroid is called a meridian ellipse (notice that ellipsoid and spheroid are equivalent and interchangeable words).

Figure 1: An oblate ellipsoid, defined by its semi-major axis a and semi-minor axis b. Many different sorts of ellipsoids have been defined. Local ellipsoids have been established to fit the Geoid (mean sea level) well over an area of local interest, which in the past was never larger than a continent. This meant that the differences between the Geoid and the reference ellipsoid could effectively be ignored, allowing accurate maps to be drawn in the vicinity of the datum (Figure 2).
With increasing demands for global surveying, global reference ellipsoids are developed. In contrast to local ellipsoids, which apply only to a specific country or localized area of the Earth’s surface, global ellipsoids (GRS80, WGS84) approximate the Geoid as a mean Earth ellipsoid.
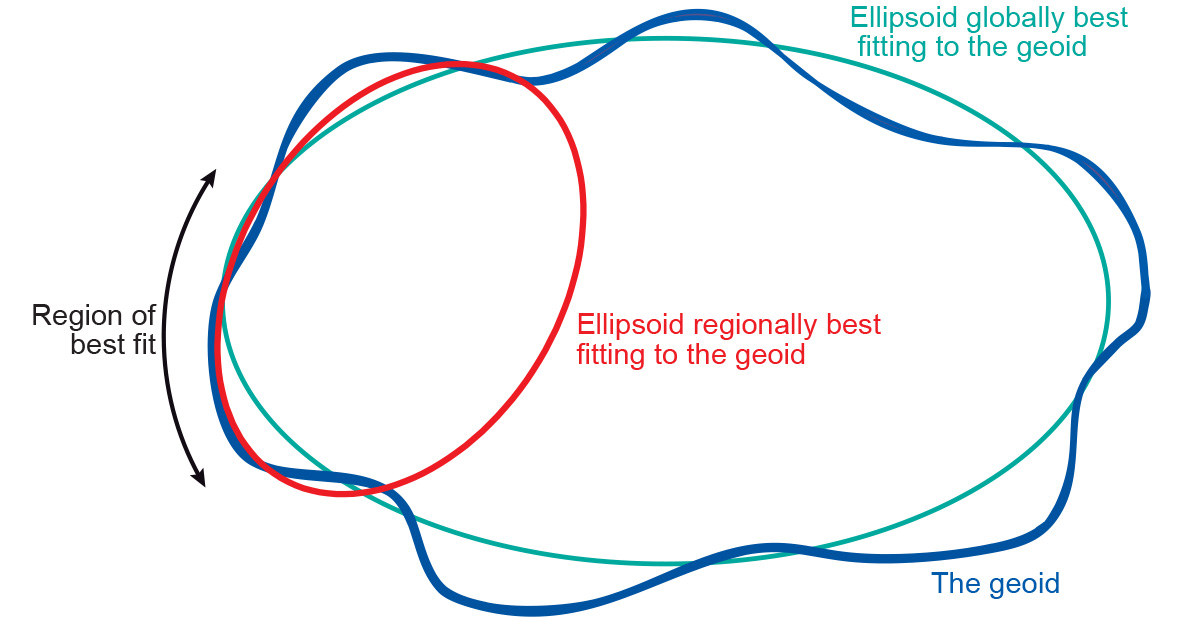
Figure 2: The Geoid, its global best-fit ellipsoid, and a regional
best-fit ellipsoid for a chosen region. Adapted from: Ordnance Survey of Great Britain. A Guide to Coordinate Systems in Great Britain. -
Reference surface
A reference surface is a datum that provide a reference point to the Earth's surface. There are horizontal datums, that describe the position on the Earth's surface and vertical datums that describe elevation. Two main reference surfaces have been established to approximate the shape of the Earth: one is called the Geoid, the other the Ellipsoid.
The surface of the Earth is far from uniform. Its oceans can be treated as reasonably uniform, but the surface or topography of its land masses exhibits large vertical variations between mountains and valleys. These variations make it impossible to approximate the shape of the Earth with any reasonably simple mathematical model.
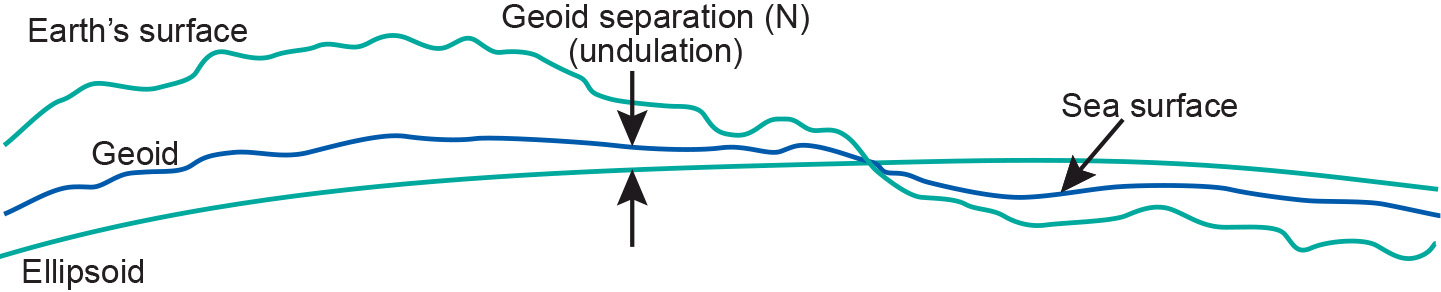
Figure: The Earth’s surface and two reference surfaces used to approximate it: the Geoid; and a reference ellipsoid. The Geoid separation (N) is the deviation between the Geoid and the reference ellipsoid. -
Global horizontal datum
In contrast to local horizontal datum systems which apply only to a specific country or localized area of the Earth’s surface, global datum systems approximate the Geoid as a mean Earth ellipsoid.
-
Geographic coordinate system
Geographic (or global) coordinate systems locate data either on the Earth’s surface in a 3D space or on the Earth’s reference surface (ellipsoid or sphere) in a 2D space. This includes: 2D Geographic Coordinates, 3D Geographic Coordinates, and 3D Geocentric Coordinates.
-
Planar coordinate system
Planar coordinate systems locate data on the flat surface of a map in a 2D space. This includes 2D Cartesian Coordinates and 2D Polar Coordinates.
-
Geoid
The Geoid is a surface defined by the height of the ocean as it would be only affected by gravity. The Geoid is used to describe heights.
-
Global vertical datum
There two different definitions of a global vertical datum:
- It is an globally defined ellipsoid used as reference surface for measuring geodetic heights.
- It is a Geoid used as reference surface for measuring orthometric heights.
Given the definition of the Geoid, global vertical datums can be defined by gravity satellites. These satellites measure the earth's gravity. The variations in gravity are converted to heights that can be compared globally all over the world (so mountain ranges in America can be measured against those in Europe). The local datum systems can be linked together which simplifies height-related issues.
-
Horizontal datum
A horizontal datum is a mathematical surface (a particular ellipsoid) used for geodetic computations and to define locations. World-wide there are several hundred of these horizontal datums defined.
In the past datum systems apply only to a specific country or localized area of the Earth’s surface. Recent years have seen that globalisation is leading to the definition of global datum systems (or geocentric datum systems), like the International Terrestrial Reference System (ITRS), and several implementations, such as ITRF2000 or WGS84.
-
Vertical datum
Vertical datums (or height datums) are reference surfaces used for measuring heights.
-
Sphere
A sphere is defined mathematically as a three-dimensional surface with every point on its surface has the same distance (radius) from its centre.

Figure: The mathematically simpler sphere may be used as reference surface for maps at small-scale. Instead of using the ellipsoid as reference surface for mapping, the sphere might be sufficient for certain mapping tasks. In practice, maps at scale 1:5,000,000 or smaller can use the mathematically simpler sphere without the risk of large distortions. At larger scales, the more complicated mathematics of ellipsoids are needed to prevent these distortions in the map.
-
Local horizontal datum
Local horizontal datums are reference surfaces (ellipsoids) that apply to a specific country or localized area of the Earth’s surface.
An ellipsoid is positioned and oriented with respect to the local mean sea level by adopting a latitude (ϕ) and longitude (λ) and ellipsoidal height (h) of what is called a fundamental point and an azimuth to an additional point. We say that this defines a local horizontal datum. Note that the term horizontal datum and geodetic datum are treated as equivalent and interchangeable terms.
-
Local vertical datum
Local vertical datums are locally defined by registering the ocean’s water level at coastal locations over several years using tide gauges (mareographs). Averaging the registrations largely eliminates variations in sea level over time. The resultant water level represents a local vertical datum, also called mean sea level. It is an approximation to the Geoid.
Several definitions of local vertical datums appear throughout the world. They are parallel to the Geoid but offset by up to a couple of metres to allow for local phenomena such as ocean currents, tides, coastal winds, water temperature and salinity at the location of the tide gauge.
Care must be taken when using heights from another local vertical datum. This might be the case, for example, in areas along the border of adjacent nations. The local vertical datum is implemented through a levelling network, which consists of benchmarks whose height above mean sea level has been determined through geodetic levelling .
-
Map projection
A map projection is a mathematically described technique for representing the Earth’s curved surface on a flat map. The actual mapping cannot usually be visualized as a true geometric projection, directly onto the mapping plane. Rather, it is achieved through mapping equations.
-
Projection classification
Many map projections have been developed, each with its own specific qualities. It is these qualities that make the resulting maps useful for certain purposes. By definition, any map projection is associated with scale distortions. There is simply no way to flatten an ellipsoidal or spherical surface without stretching some parts of the surface more than others. The amount and kind of distortions a map has depends on the type of map projection.
Classification can be based on:
-
Mean sea level
It is mentioned in Geoid that in order to establish the Geoid as a reference for heights, the ocean’s water level is registered at coastal locations over several years and averaged to eliminate variations in sea level over time. The resultant water level represents an approximation to the Geoid and is termed mean sea level. Local mean sea levels (also called local vertical datums) are parallel to the Geoid but offset by up to a couple of metres to allow for local phenomena such as ocean currents, tides, coastal winds, water temperature and salinity at the location of the tide gauge. Several definitions of local mean sea levels appear throughout the world.
-
Spatial Reference System
A spatial reference system or coordinate reference system is a coordinate-based system used to position objects, either on the earth’s surface in a 3D space, or on the earth’s reference surface in a 2D space, or on the other hand on the flat surface of the map in a 2D space. Many different sorts of spatial reference systems exist, the most widely used are the geographic coordinate systems and map coordinate systems. A geographic coordinate system is a global system which consists of two angles, the latitude angle and the longitude angle. A map coordinate system is a 2D Cartesian coordinate system (x,y) that defines a specific map projection.
-
Projection class
Some map projections can be visualized as true geometric projections directly onto the mapping plane—known as an azimuthal projections—or onto an intermediate surface, which is then rolled out onto the mapping plane. Typical choices for such intermediate surfaces are cones and cylinders. These map projections are called conical or cylindrical projections, respectively.
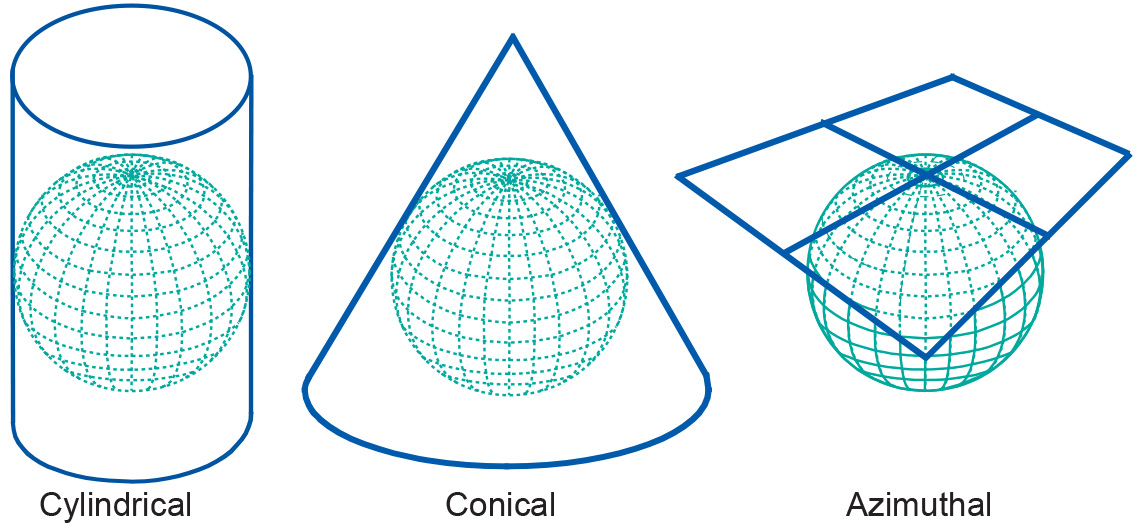
Figure: Classes of map projections by geometry The azimuthal, conical, and cylindrical surfaces in the picture are all tangent surfaces, i.e. they touch the horizontal reference surface at one point (azimuthal), or along a closed line (cone and cylinder), only.
-
Projections by secancy
Another class of projections is obtained if the surfaces are chosen to be secant to (to intersect with) the horizontal reference surface. Then, the reference surface is intersected along one closed line (azimuthal) or two closed lines (cone and cylinder). Secant map surfaces are used to reduce or average out scale errors since the line(s) of intersection are not distorted on the map.
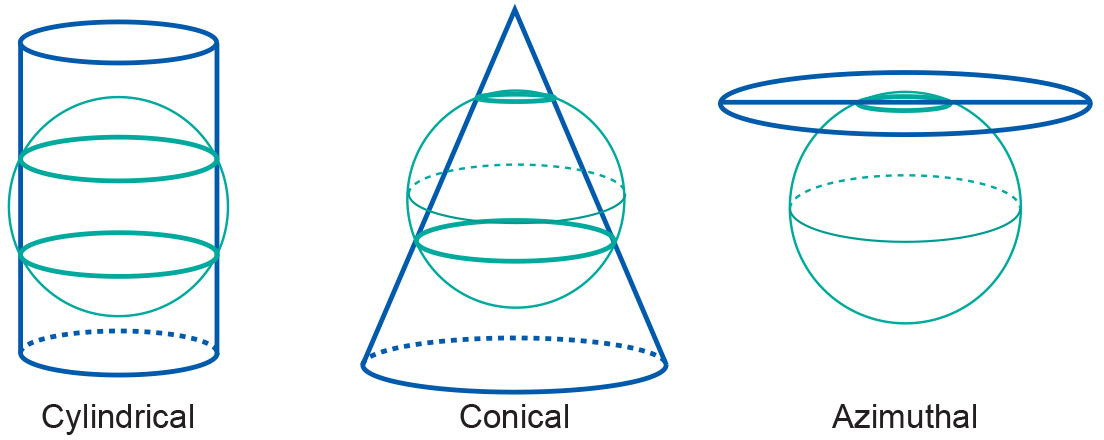
Figure: Three classes of secant projection -
Projections by aspect
Projections can also be described in terms of the direction of the projection plane's orientation (whether cylinder, plane or cone) with respect to the globe. This is called the aspect of a map projection. The three possible aspects are normal, transverse and oblique. In a normal projection, the main orientation of the projection surface is parallel to the earth's axis (as in the figure below for the cylinder and the cone). A transverse projection has its main orientation perpendicular to the earth's axis. Oblique projections are all other, non-parallel and non-perpendicular, cases.
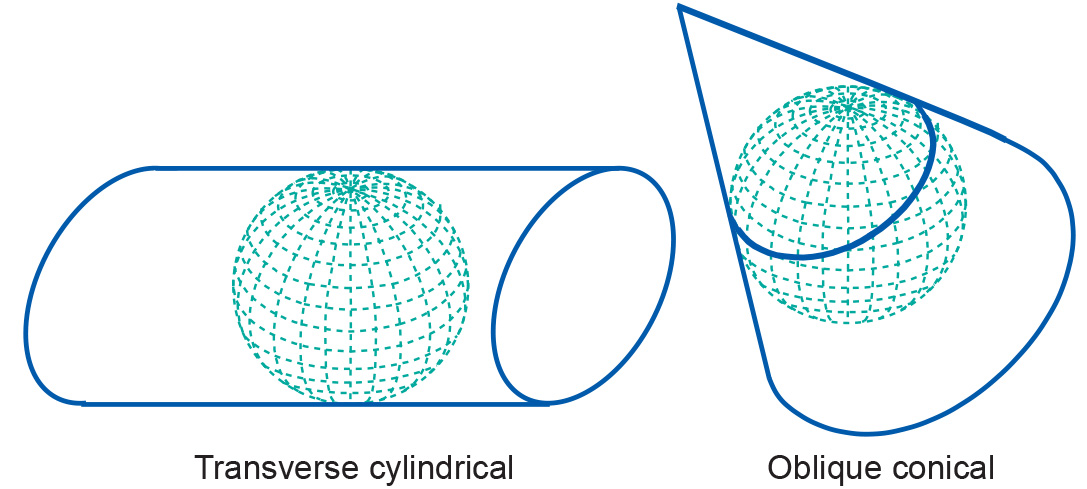
Figure: A transverse cylindrical and an oblique conical projection -
Projections by distortion property
How the Earth's surface is projected onto the plane, cone or cylinder determines which kind of distortion properties the map will have compared to the original curved reference surface.
The distortion properties of map are typically classified according to what is not distorted on the map:
-
In a conformal map projection (orthomorphic) the angles between lines in the map are indentical to the angles between the original lines on the curved reference surface. This means that angles (with short sides) and shapes (of small areas) are shown correctly on the map.
-
In an equal-area (equivalent) map projection the areas in the map are identical to the areas on the curved reference surface (taking into account the map scale), which means that areas are represented correctly on the map.
-
In an equidistant map projection the length of particular lines in the map are the same as the length of the original lines on the curved reference surface (taking into account the map scale).
A particular map projection can have any one of these three properties. No map projection can be both conformal and equal-area. A projection can only be equidistant (true to scale) at certain places or in certain directions.
-
-
Mapping equations
The actual mapping cannot usually be visualized as a true geometric projection, directly onto the mapping plane. Rather, it is achieved through mapping equations.