Error propagation
Introduction
The acquisition of high quality base data still does not guarantee that the results of further, complex processing can be treated with certainty. As the number of processing steps increases, it becomes more difficult to predict the behaviour of such error propagation. These various errors may affect the outcome of spatial data manipulations. In addition, further errors may be introduced during the various processing steps.
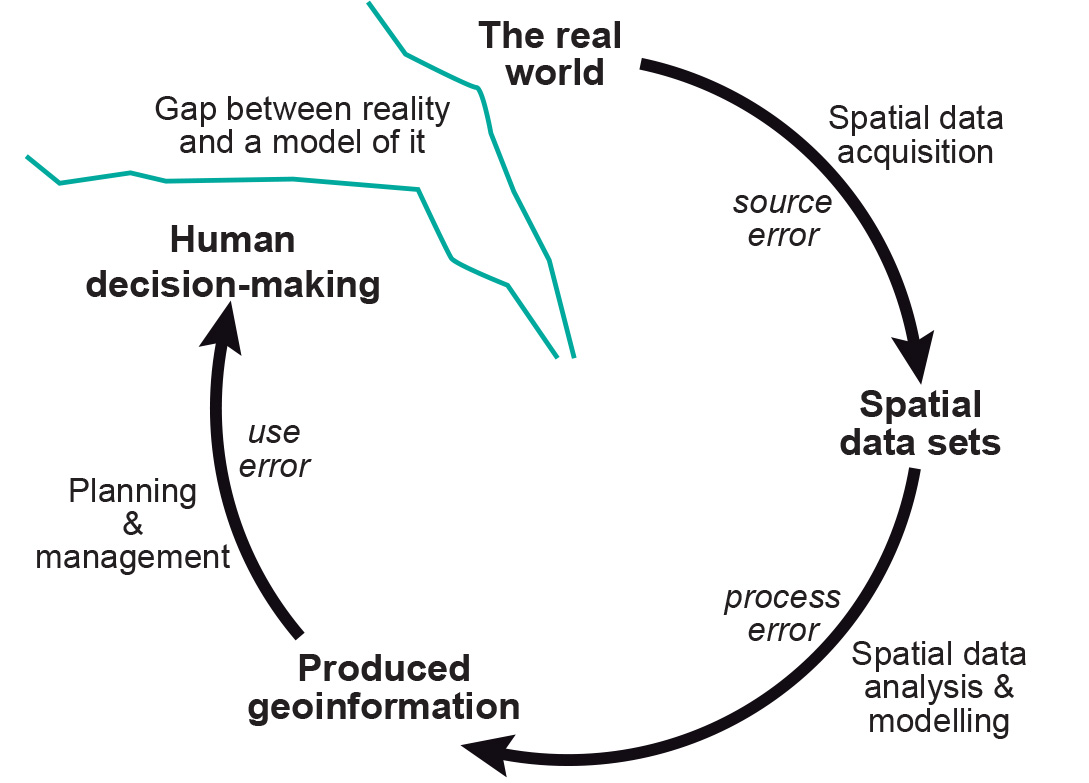
Explanation
Quantifying error propagation
Chrisman (1989) noted that:
We will never be able to capture and represent everything that happens in the real world perfectly in a
-
testing the accuracy of each state by measurement against the real world; and
-
error propagation modelling, either analytically or by means of simulation techniques.
Common Sources of Error in GIS
This table lists some common sources of error that may be introduced into
| Coordinate adjustments | Generalization |
| - rubber sheeting/transformations | - linear alignment |
| - projection changes | - line simplification |
| - datum conversions | - addition/deletion of vertices |
| - rescaling | - linear displacement |
| Feature Editing | Raster/Vector Conversions |
| - line snapping | - raster cells to polygons |
| - extension of lines to intersection | - polygons to raster cells |
| - reshaping | - assignment of point attributes |
| - moving/copying | - to raster cells |
| - elimination of spurious polygons | - post-scanner line thinning |
| Attribute editing | Data input and Management |
| - numeric calculation and change | - digitizing |
| - text value changes/substitution | - scanning |
| - re-definition of attributes | - topological construction / spatial indexing |
| - attribute value update | - dissolving polygons with same attributes |
| Boolean Operations | Surface modelling |
| - polygon on polygon | - contour/lattice generation |
| - polygon on line | - TIN formation |
| - polygon on point | - Draping of data sets |
| - line on line | - -section/profile generation |
| - overlay and erase/update | - Slope/aspect determination |
| Display and Analysis | Display and Analysis |
| - cluster analysis | - class intervals choice |
| - calculation of surface lengths | - areal interpolation |
| - shortest route/path computation | - perimeter/area size/volume computation |
| - buffer creation | - distance computation |
| - display and query | - spatial statistics |
| - adjacency/contiguity | - label/text placement |
Error propagation modelling
Error propagation can be modelled mathematically, although these models are very complex and only valid for certain types of data(e.g. numerical attributes). Rather than explicitly modelling error propagation, it is often more practical to test the results of each step in the process against some independently measured reference data.
It is important to distinguish models of error from models of error propagation in
In other words, we would like to know how errors in the source data behave under the manipulations that we subject them to in a
Initially, error propagation models described only the propagation of attribute error (Heuvelink, 1993; Veregin, 1995). More recent research has addressed the spatial aspects of error propagation and the development of models incorporating both attribute and location components. These topics are beyond the scope of this book and readers are referred to Arbia et al. (1998) and Kiiveri (1997) for more details.
Examples
One of the most commonly applied operations in
Consider another example. A land use planning agency is faced with the problem of identifying areas of agricultural land that are highly susceptible to erosion. Such areas occur on steep slopes in areas of high rainfall. The spatial data used in a
-
a land use map produced five years previously from 1:25,000 scale aerial photographs;
-
a
DEM produced by interpolating contours from a 1:50,000 scale topographic map; and -
annual rainfall statistics collected with two rainfall gauges.
The reader is invited to assess what sort of errors are likely to occur in this analysis.
External resources
- Arbia, G., Griffith, D. & Haining, R. (1998). Error propagation modelling in raster gis: overlay operations. International Journal of Geographical Information Science, 12(2), 145-167. doi:10.1080/136588198241932
- Chrisman, N.R. (1989). Errors in cartegorical maps: testing versus simulation. In Auto carto 9 : proceedings 9th international symposium on computer - assisted cartography: Baltimore, Maryland April 2 - 7, 1989, pp. 521-529. Bethesda: ASPRS and ACSM.
- Heuvelink, G.B.M. (1993). Error propegation in quantitive spatial modelling: applications in geographical information systems. Netherlands Geographical Studies (163). Amsterdam: KNAG. Utrecht: Faculteit Ruimtelijke Wetenschappen UU.
- Kiiveri, H.T. (1997). Assessing, representing and transmitting positional accuracy in maps. International Journal of Geographical Information Systems, 11(1) , 33-52. doi:10.1080/136588197242482.
-
Veregin, H. (1995). Developing and testing of an error propagation model for GIS overlay operations. International Journal of Geographical Information Systems 9(6), 595-619. doi: 10.1080/02693799508902059.
Developing and testing of an error propagation model for GIS overlay operations
Learning outcomes
-
14 - Data quality: data handling
Identify the impact of Geo-information handling on data quality (level 1).
-
15 - Data quality: quality assessment
Student is abel to explain and apply quality assessment procedures (level 1, 2 and 3).
Prior knowledge
Self assessment
Referring back to the Figure above, the reader is also encouraged to reflect on errors introduced in the components of the application models, specifically, the methodological aspects of representing geographic phenomena. What might be the consequences of using a random function in an urban transportation model (when, in fact, travel behaviour is not purely random)?
Outgoing relations
- Error propagation is related to Data Quality