15 - Data quality: quality assessment
Student is abel to explain and apply quality assessment procedures (level 1, 2 and 3).
Concepts
-
Accuracy
The accuracy of a single measurement can be defined as:
the closeness of observations, computations or estimates to the true values or the values perceived to be true (United States Geological Survey, 1990)An accurate measurement has a mean close to the true value. Measurement errors are generally described in terms of accuracy. In the case of spatial data, accuracy may relate not only to the determination of coordinates (positional error) but also to the measurement of quantitative attribute data. This can include positional accuracy, temporal accuracy, or attribute accuracy.
In the case of surveying and mapping, the “truth” is usually taken to be a value obtained from a survey of higher accuracy, for example by comparing photogrammetric measurements with the coordinates and heights of a number of independent check points determined by field survey. Although it is useful for assessing the quality of definite objects, such as cadastral boundaries, this definition clearly has practical difficulties in the case of natural resource mapping where the “truth” itself is uncertain, or boundaries of phenomena become fuzzy.
Prior to the availability of
GPS , resource surveyors working in remote areas sometimes had to be content with ensuring an acceptable degree of relative accuracy among the relative and absolute accuracy measured positions of points within the surveyed area. If location and elevation are fixed with reference to a network of control points that are assumed to be free of error, then the absolute accuracy of the survey can be determined. -
Perkal band
As a line is composed of an infinite number of points, confidence limits can be described by what is known as an epsilon (ε) or Perkal band at a fixed distance on either side of the line (Figure 1).
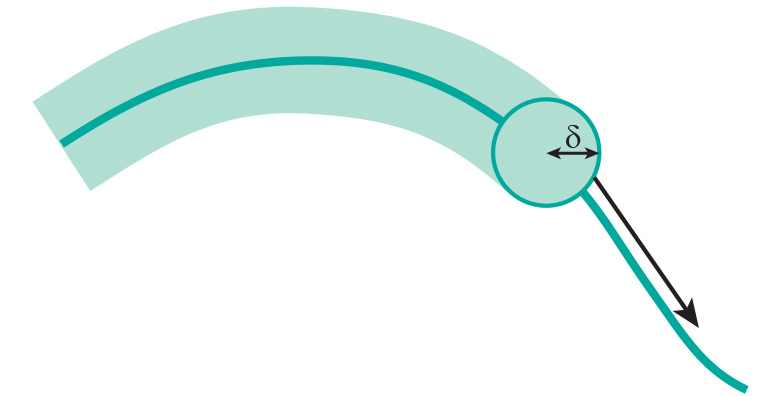
Figure 1: The ε or Perkal band is formed by rolling an imaginary circle of a given radius along a line. The width of the band is based on an estimate of the probable location error of the line, for example to reflect the accuracy of manual digitizing. The epsilon band may be used as a simple means for assessing the likelihood that a point receives the correct attribute value (Figure 2).
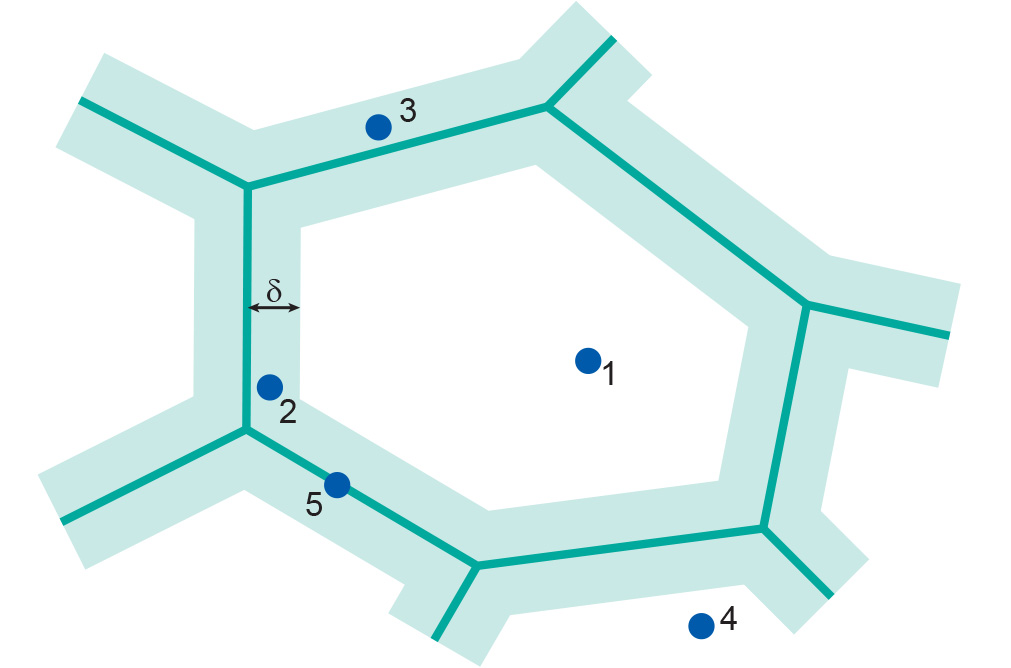
Figure 2: The ε band may be used to assess the likelihood that a point falls within a particular polygon (source: Openshaw et al. (1991). Point 3 is less likely part of the middle polygon than point 2. -
RMSE
Positional accuracy is normally measured as a root mean square error (RMSE). The RMSE is similar to, but not to be confused with, the standard deviation of a statistical sample.
-
Attribute accuracy
We can identify two types of attribute accuracies. These relate to the type of data we are dealing with:
-
For nominal or categorical data, the accuracy of labelling (for example the type of land cover, road surface, etc).
-
For numerical data, numerical accuracy (such as the concentration of pollutants in a soil, height of trees in forests, etc).
It follows that depending on the data type, assessment of attribute accuracy may range from a simple check on the labelling of features - for example, is a road classified as a metalled road actually surfaced or not? - to complex statistical procedures for assessing the accuracy of numerical data, such as the percentage of pollutants present in a soil.
-
-
Data Quality
With the advent of satellite remote sensing,
GPS and GIS technology, and the increasing availability of digital spatial data, resource managers and others who formerly relied on the surveying and mapping profession to supply high quality map products are now in a position to produce maps themselves. At the same time,GIS s are being increasingly used for decision-support applications, with increasing reliance on secondary data sourced through data providers or via the internet, from geo-webservices. The consequences of using low-quality data when making important decisions are potentially grave. There is also a danger that uninformedGIS users will introduce errors by incorrectly applying geometric and other transformations to the spatial data held in their database.We discuss positional, temporal and attribute accuracy, lineage, completeness, and logical consistency.
-
Error matrix
When spatial data are collected in the field, it is relatively easy to check on the appropriate feature labels. In the case of remotely sensed data, however, considerable effort may be required to assess the accuracy of the classification procedures. This is usually done by means of checks at a number of sample points. The field data are then used to construct an error matrix (also known as a confusion or misclassification matrix) that can be used to evaluate the accuracy of the classification. An example is provided in the Table below, where three land use types are identified. For 62 check points that are forest, the classified image identifies them as forest. However, two forest check points are classified in the image as agriculture. Vice versa, five agriculture points are classified as forest. Observe that correct classifications are found on the main diagonal of the matrix, which sums up to 92 correctly classified points out of 100 in total.
Table: Example of a simple error matrix for assessing map attribute accuracy. The overall accuracy is (62 + 18 + 12) ∕ 100 = 92%. Classified image Reference data Forest Agriculture Urban Total Forest 62 5 0 67 Agriculture 2 18 0 20 Urban 0 1 12 13 Total 64 24 12 100 -
Sources of errors
The surveying and mapping profession has a long tradition of determining and minimizing errors. This applies particularly to land surveying and photogrammetry, both of which tend to regard positional and height errors as undesirable. Cartographers also strive to reduce geometric and attribute errors in their products, and, in addition, define quality in specifically cartographic terms, for example quality of line work, layout, and clarity of text.
It must be stressed that all measurements made with surveying and photogrammetric instruments are subject to error. These include:-
Human Errors in measurement (e.g. reading errors) generally referred to as gross errors or blunders. These are usually large errors resulting from carelessness, which could have been avoided through careful observation, although it is never absolutely certain that all blunders could have been avoided or eliminated.
-
Instrumental or Systematic Errors (e.g. due to maladjustment of instruments). This leads to errors that vary systematically in sign and/or magnitude, but can go undetected by repeating the measurement with the same instrument. Systematic errors are particularly dangerous because they tend to accumulate.
-
So–called Random Errors caused by natural variations in the quantity being measured. These are effectively the errors that remain after blunders and systematic errors have been removed. They are usually small, and dealt with in least–squares adjustment.
Measurement errors are generally described in terms of accuracy.
-
-
Completeness
Completeness refers to whether there are data lacking in the database compared to what exists in the real world. Essentially, it is important to be able to assess what does and what does not belong to a complete data set as intended by its producer. It might be incomplete (i.e. it is “missing” features which exist in the real world), or overcomplete (i.e. it contains “extra” features which do not belong within the scope of the data set as it is defined).
Completeness can relate to either spatial, temporal, or thematic aspects of a data set. For example, a data set of property boundaries might be spatially incomplete because it contains only 10 out of 12 suburbs; it might be temporally incomplete because it does not include recently subdivided properties; and it might be thematically overcomplete because it also includes building footprints.
-
Lineage
Lineage describes the history of a data set. In the case of published maps, some lineage information may be provided as part of its meta-data, in the form of a note on the data sources and procedures used in the compilation of the data. Examples include the date and scale of aerial photography, and the date of field verification. Especially for digital data sets, however, lineage may be defined more formally as:
“that part of the data quality statement that contains information that describes the source of observations or materials, data acquisition and compilation methods, conversions, transformations, analyses and derivations that the data has been subjected to, and the assumptions and criteria applied at any stage of its life (Clarke and Clark, 1995).”
All of these aspects affect other aspects of quality, for example positional accuracy. Clearly, if no lineage information is available, it is not possible to adequately evaluate the quality of a data set in terms of “fitness for use”.
-
Logical consistency
For any particular application, (predefined) logical rules (consistency) concern:
-
the compatibility of data with other data in a data set (e.g. in terms of data format);
-
the absence of any contradictions within a data set;
-
the topological consistency of the data set; and
-
the allowed attribute value ranges, as well as combinations of attributes. For example, attribute values for population, area and population density must agree for all entities in the database.
The absence of any inconsistencies does not necessarily imply that the data are accurate.
-
-
Positional accuracy
The surveying and mapping profession has a long tradition of determining and minimizing error. Measurement errors are generally described in terms of accuracy. The general ways of quantifying positional accuracy is by using
RMSE .Accuracy should not be confused with precision, which is a statement of the smallest unit of measurement to which data can be recorded. In conventional surveying and mapping practice, accuracy and precision are closely related. Instruments with an appropriate precision are employed, and surveying methods chosen, to meet specified tolerances in accuracy. In
GIS s, however, the numerical precision of computer processing and storage usually exceeds the accuracy of the data. This can give rise to what is known as spurious accuracy.The relationship between accuracy and precision can be clarified using graphs that display the probability distribution (see below) of a measurement against the true value T. In the Figure below, we depict the cases of good/bad accuracy against good/bad precision.
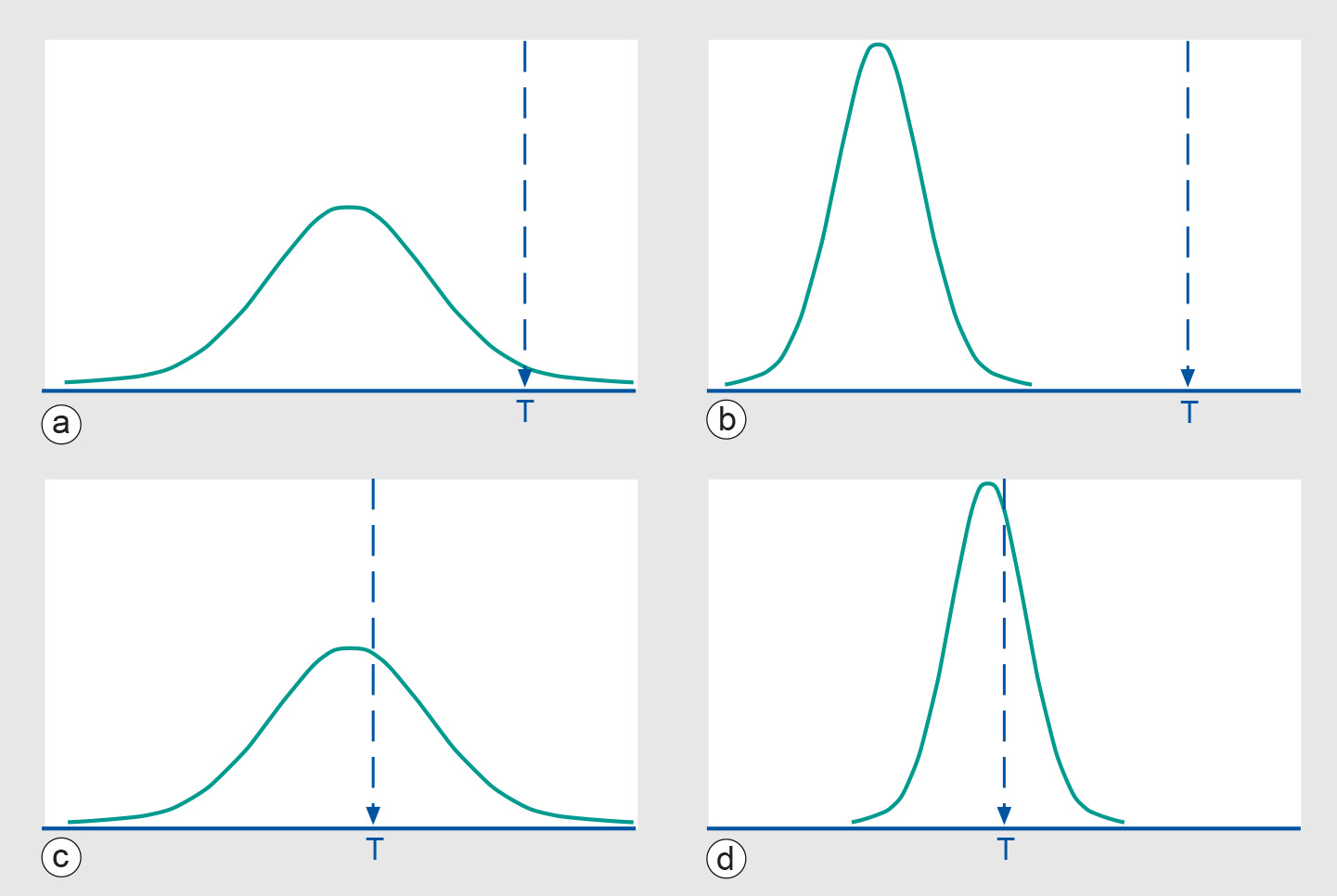
Figure: A measurement probability function and the underlying true value T: (a) bad accuracy and precision, (b) bad accuracy/good precision, (c) good accuracy/bad precision, and (d) good accuracy and precision. -
Precision
Precision is a statement of the smallest unit of measurement to which data can be recorded. A precise measurement has a sufficiently small variance. Another way of saying this is that the range in which the data falls is sufficiently small.
-
Temporal accuracy
The amount of spatial data sets and archived remotely-sensed data has increased enormously over the last decade. These data can provide useful temporal information, such as changes in land ownership and the monitoring of environmental processes such as deforestation. Analogous to its positional and attribute components, the quality of spatial data may also be assessed in terms of its temporal accuracy. For a static feature this refers to the difference in the values of its coordinates at two different times.
Temporal accuracy includes not only the accuracy and precision of time measurements (for example, the date of a survey) but also the temporal consistency of different data sets. Because the positional and attribute components of spatial data may change together or independently, it is also necessary to consider their temporal validity. For example, the boundaries of a land parcel may remain fixed over a period of many years whereas the ownership attribute may change more frequently.
-
Membership functions
There are many situations, particularly in surveys of natural resources, where, according to Burrough and Frank (1996, p.16), “practical scientists, faced with the problem of dividing up undividable complex continua have often imposed their own crisp structures on the raw data”. In practice, the results of classification are normally combined with other categorical layers and continuous field data to identify, for example, areas suitable for a particular land use. In a GIS, this is normally achieved by overlaying the appropriate layers using logical operators.
Particularly in the case of natural resource maps, the boundaries between units may not actually exist as lines but only as transition zones, across which one area continuously merges into another. In these circumstances, rigid measures of positional accuracy, such as RMSE, may be virtually insignificant in comparison to the uncertainty inherent in vegetation and soil boundaries, for example.
-
Error propagation
The acquisition of high quality base data still does not guarantee that the results of further, complex processing can be treated with certainty. As the number of processing steps increases, it becomes more difficult to predict the behaviour of such error propagation. These various errors may affect the outcome of spatial data manipulations. In addition, further errors may be introduced during the various processing steps.
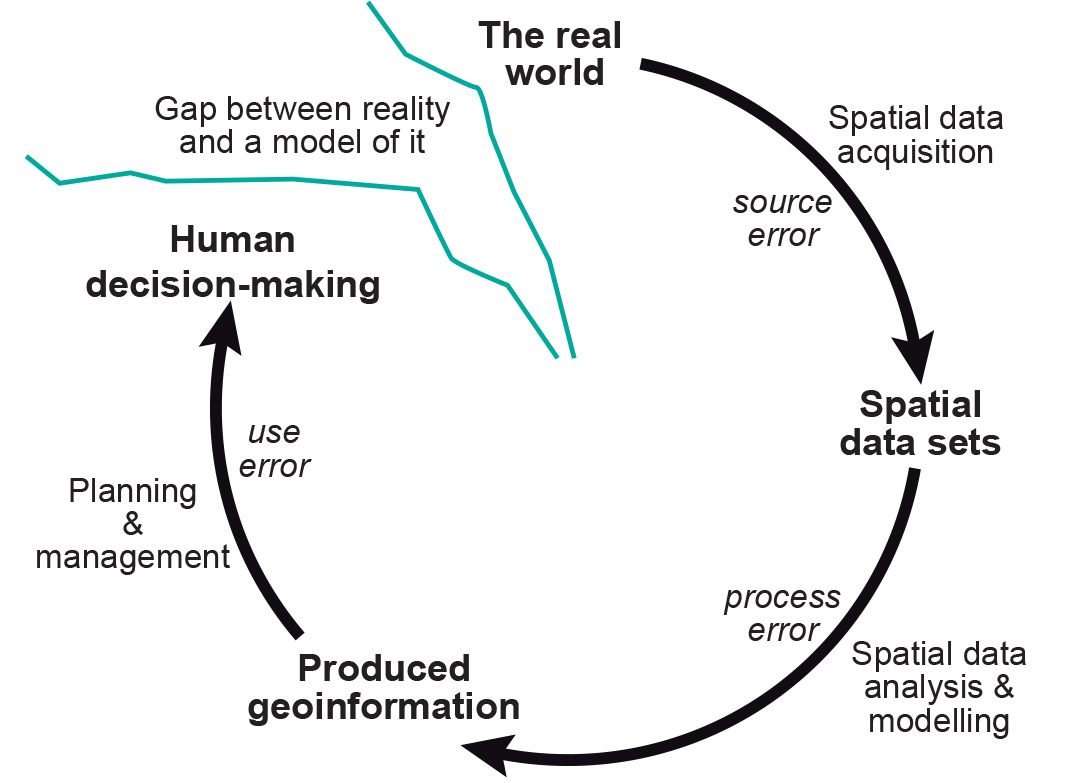
Figure: Error propagation in spatial data handling.