Topology

Topology refers to the spatial relationships between geographic elements in a data set that do not change under a continuous transformation. This is defined by topological relationships.

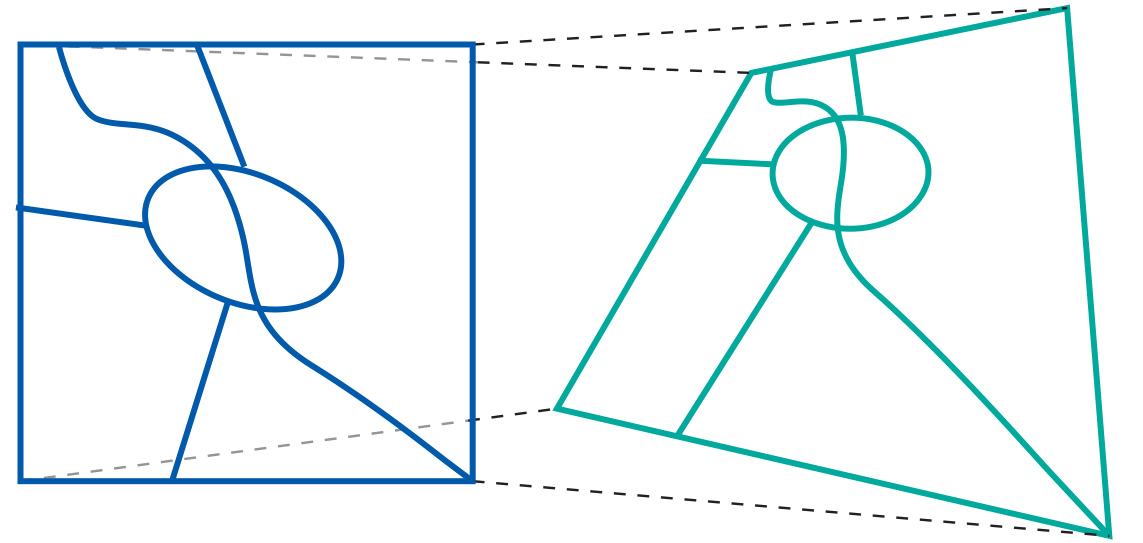
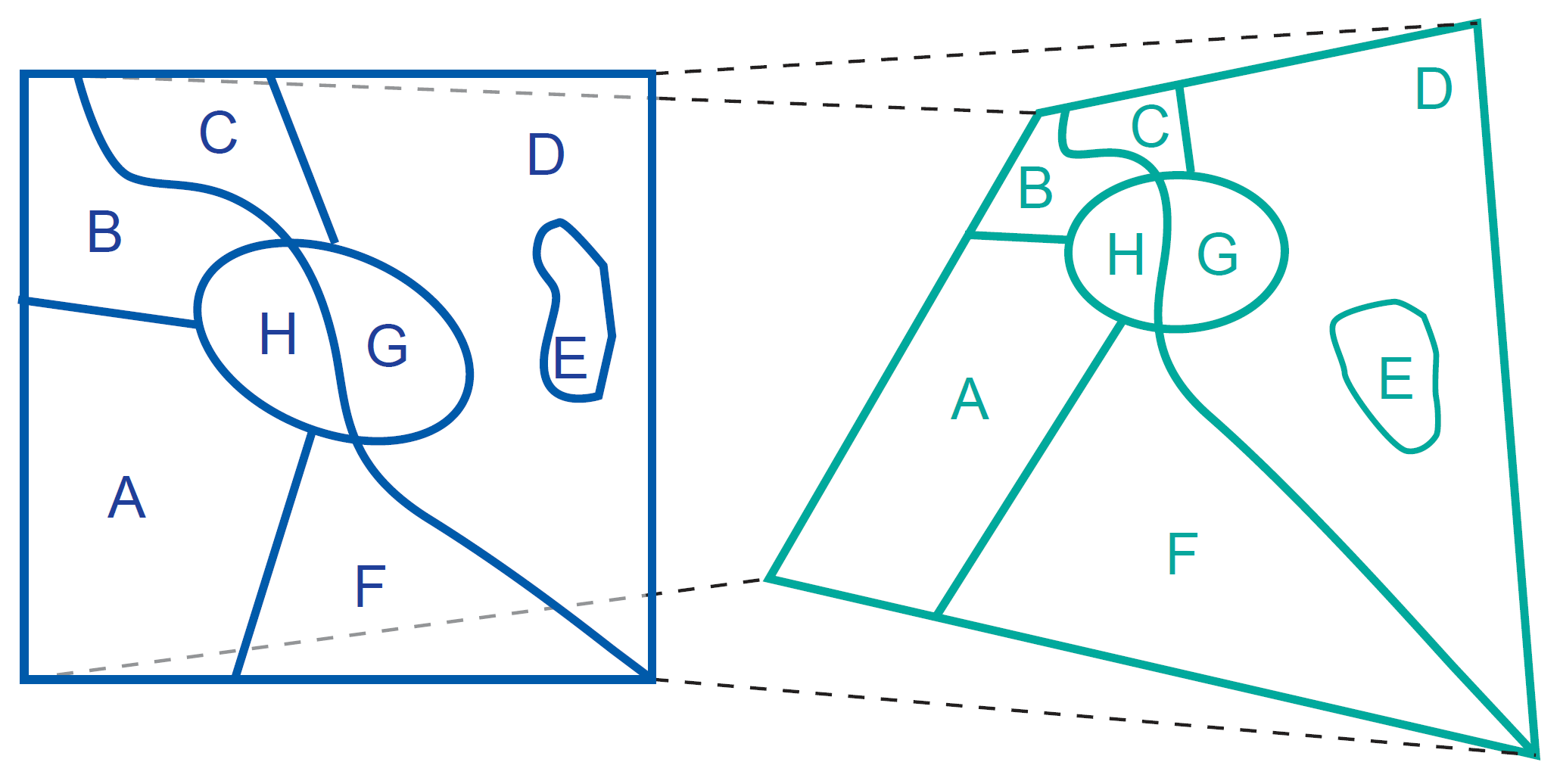
Topology deals with spatial properties that do not change under specific transformations. Take features (as in Figure 1) drawn on a sheet of rubber. These features can be made to change in shape and size by stretching and pulling the sheet, yet some properties of these features will not change:

• area E is still inside area D;

• the neighbourhood relationships between A, B, C, D, and E stay intact, and their boundaries have the same start and end nodes;

• the areas are still bounded by the same boundaries, only the shapes and lengths of their perimeters have changed.

Topological relationships are built from simple elements into more complex elements: nodes define line segments, and line segments connect to define lines, which in turn define polygons. Issues relating to order, connectivity and adjacency of geographical elements form the basis of more sophisticated GIS analyses. These relationships (called topological properties) are invariant under a continuous transformation and are referred to as a topological mapping.

We will now consider topological aspects in two ways. Firstly, using simplices, we will look at how simple elements define more complex ones. Secondly, we will examine the logical aspects of topological relationships using set theory. The three-dimensional case is also briefly discussed.

The mathematical properties of the geometric space used for spatial data may be described as follows:

• The space is a 3D Euclidean space in which we can determine for every point its coordinates as a triple (x, y, z) of real numbers. In this space, we can define features such as points, lines, polygons and volumes as geometric primitives of the respective dimension. A point is a zero-dimensional, a line a one-dimensional, a polygon a two-dimensional, and a volume a three-dimensional primitive.

• The space is a metric space, which means that we can always compute the distance between two points according to a given distance function. Such a function is also known as a metric.

• The space is a topological space, the definition of which is a bit complicated. In essence, for every point in the space we can find a neighbourhood around it that fully belongs to that space as well.

• Interiors and boundaries are properties of spatial features that remain invariant under topological mappings. This means that, under any topological mapping, the interior and the boundary of a feature remains unbroken and intact.

Features of Topological Space

A number of advantages exist when our computer representations of geographic phenomena have built-in sensitivity to topological issues. Questions related to the “neighbourhood” of an area are a case in point. To obtain some “topological sensitivity”, simple building blocks have been proposed with which more complicated representations can be constructed:

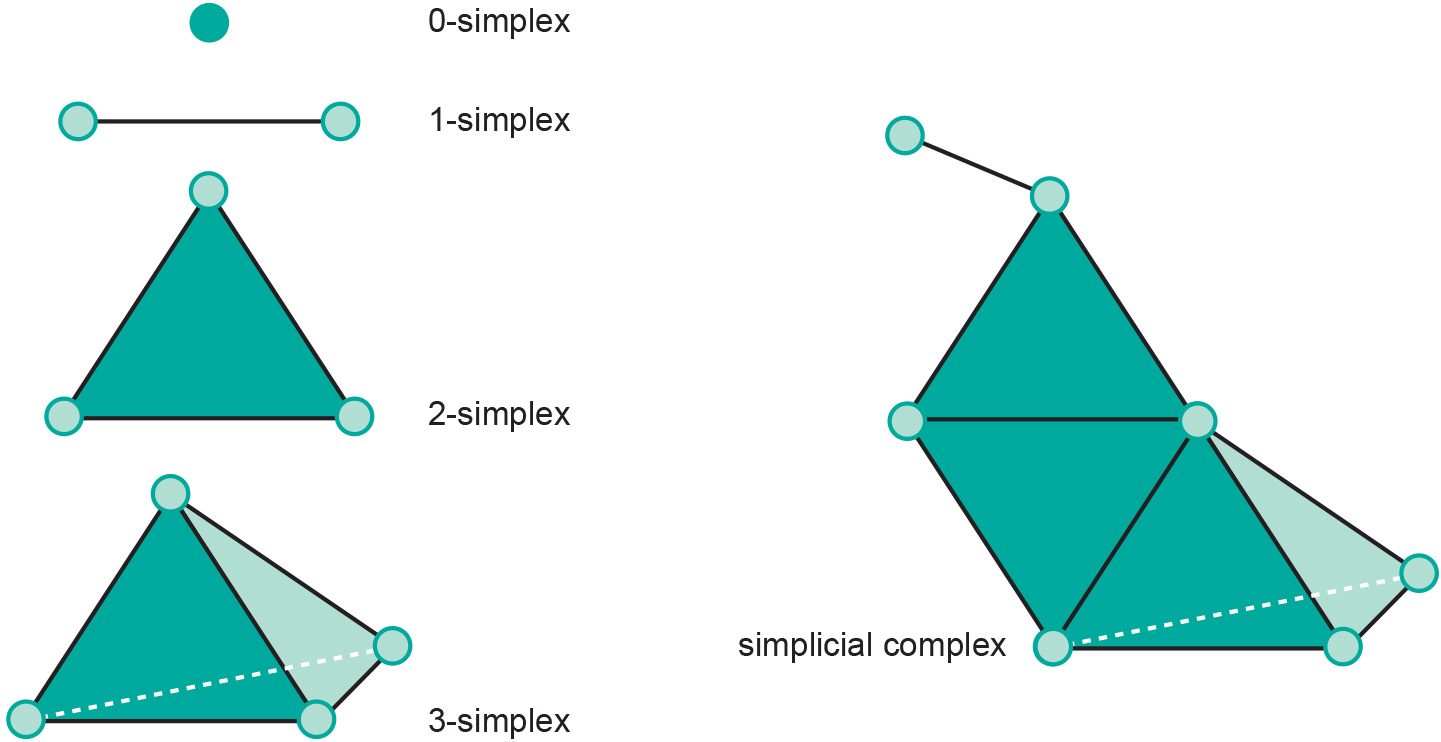
We can define features within the topological space that are easy to handle and that can be used as representations of geographic objects. These features are called simplices as they are the simplest geometric shapes of some dimension:

• point (0-simplex),

• line segment (1-simplex),

• triangle (2-simplex),

• and tetrahedron (3-simplex).

When we combine various simplices into a single feature, we obtain a simplicial complex (see Figure 2 for examples).

As the topological characteristics of simplices are well-known, we can infer the topological characteristics of a simplicial complex from the way it was constructed.