Topological relationship

We can use the topological properties of interiors and boundaries to define relationships between spatial features. Since the properties of interiors and boundaries do not change under topological mapping, we can investigate their possible relations between spatial features. We can define the interior of a region, R, as the largest set of points of R for which we can construct a disc-like environment around it (no matter how small) that also falls completely inside R. The boundary of R is the set of those points belonging to R that do not belong to the interior of R, i.e. one cannot construct a disc-like environment around such points that still belongs to R completely.

Let us consider a spatial region A. It has a boundary and an interior, both seen as (infinite) sets of points, which are denoted by boundary(A) and interior(A), respectively. We consider all possible combinations of intersections (∩) between the boundary and the interior of A with those of another region, B, and test whether they are the empty set (∅) or not. From these intersection patterns, we can derive eight (mutually exclusive) spatial relationships between two regions. If, for instance, the interiors of A and B do not intersect, but their boundaries do, yet the boundary of one does not intersect the interior of the other, we say that A and B meet. In mathematics, we can therefore define the “meets relationship” using set theory as:

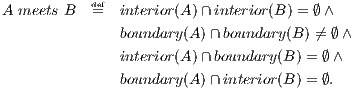
In the above formula, the symbol ∧ expresses the logical connective “and”. Thus, the formula states four properties that must all hold for the formula to be true.

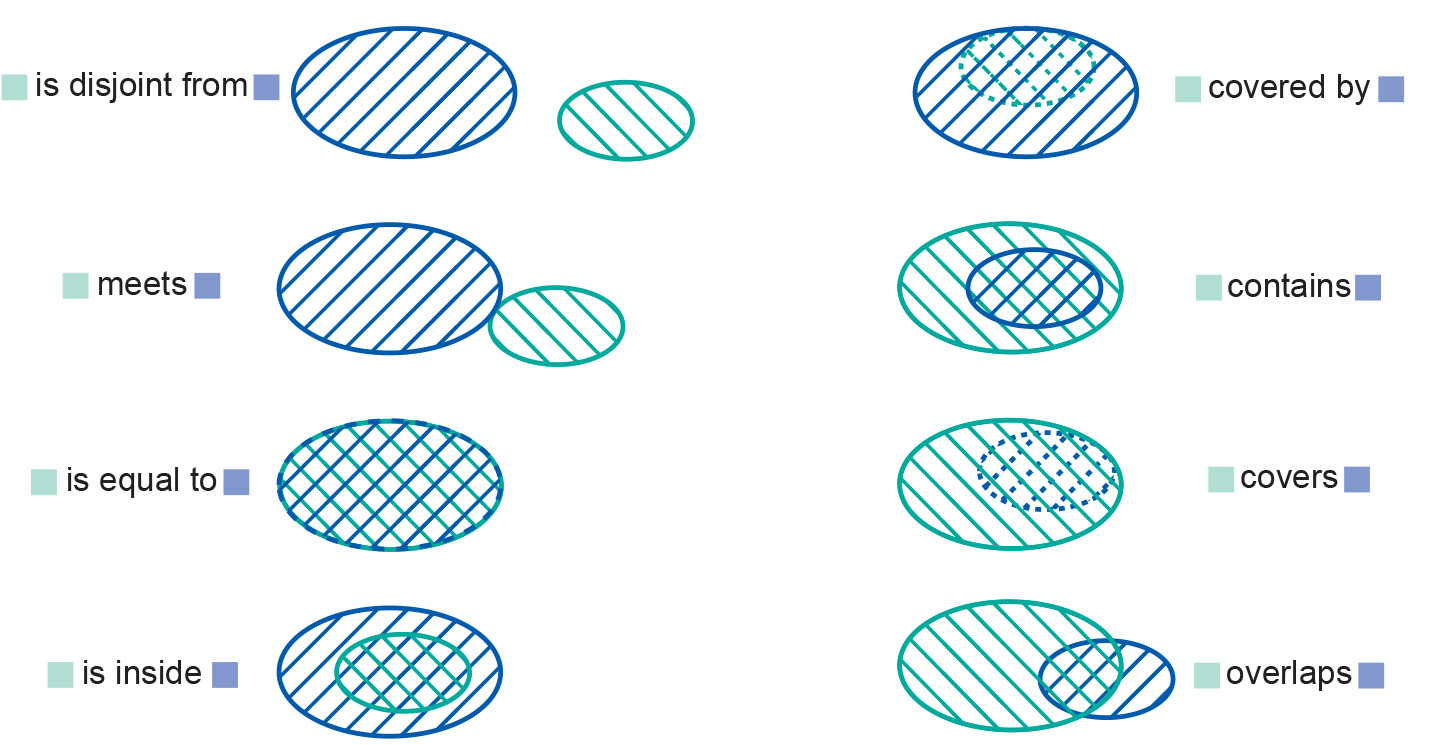
The Figure below shows all eight spatial relationships: disjoint, meets, equals, inside, covered by, contains, covers and overlaps.