Open map List

Positional accuracy

Introduction

The surveying and mapping profession has a long tradition of determining and minimizing error. Measurement errors are generally described in terms of accuracy. The general ways of quantifying positional accuracy is by using RMSE.

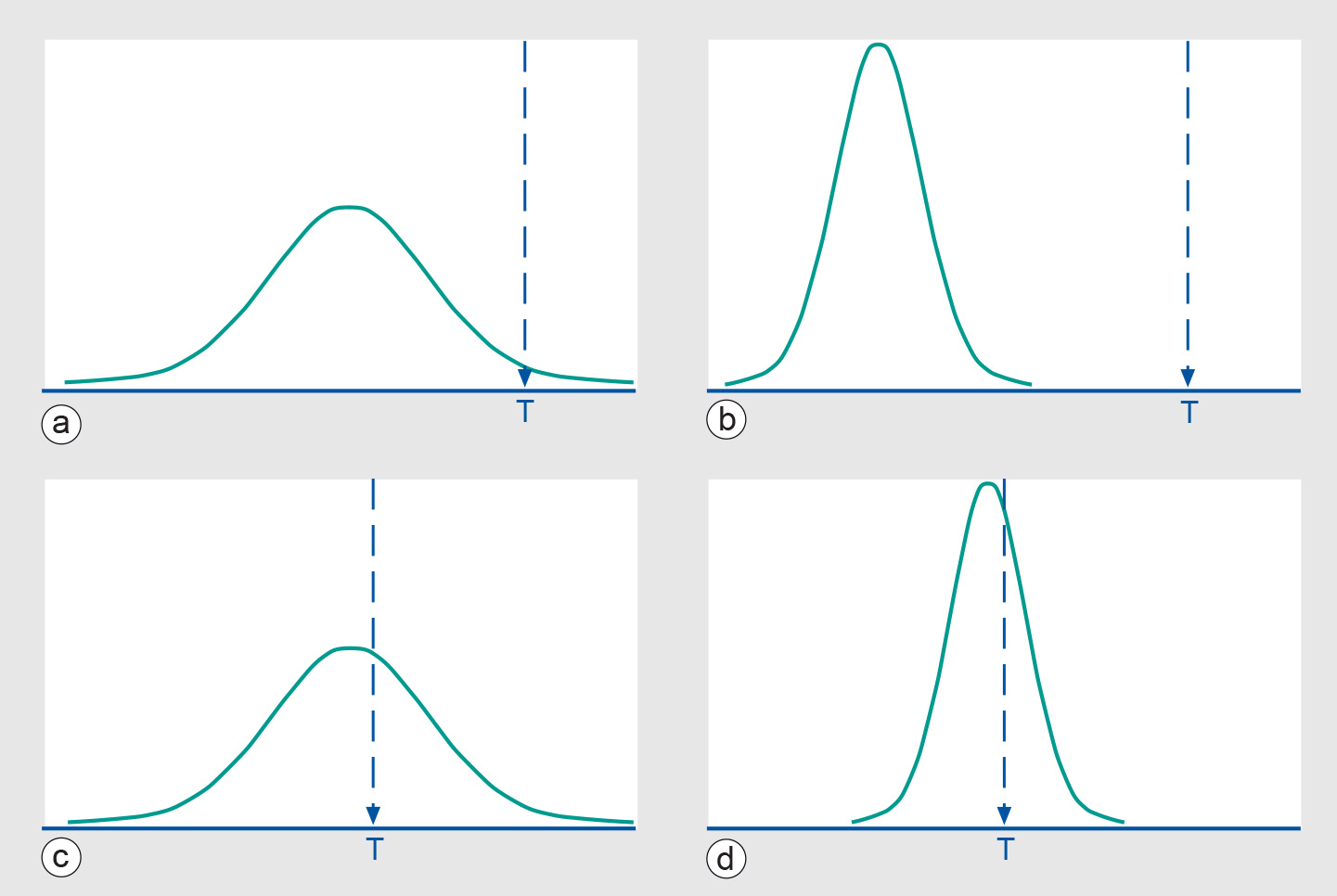
Accuracy should not be confused with precision, which is a statement of the smallest unit of measurement to which data can be recorded. In conventional surveying and mapping practice, accuracy and precision are closely related. Instruments with an appropriate precision are employed, and surveying methods chosen, to meet specified tolerances in accuracy. In GISs, however, the numerical precision of computer processing and storage usually exceeds the accuracy of the data. This can give rise to what is known as spurious accuracy.

The relationship between accuracy and precision can be clarified using graphs that display the probability distribution (see below) of a measurement against the true value T. In the Figure below, we depict the cases of good/bad accuracy against good/bad precision.

Figure: A measurement probability function and the underlying true value T: (a) bad accuracy and precision, (b) bad accuracy/good precision, (c) good accuracy/bad precision, and (d) good accuracy and precision.

Learning outcomes

15 - Data quality: quality assessment

Student is abel to explain and apply quality assessment procedures (level 1, 2 and 3).

Prior knowledge

Outgoing relations

Positional accuracy is a property of Spatial data layer
Positional accuracy is based on Sources of errors
Positional accuracy is defined by Precision
Positional accuracy is defined by Uncertainty
Positional accuracy is measured by Perkal band
Positional accuracy is measured by RMSE
Positional accuracy is part of Accuracy

Learning paths