Open map List

Perkal band

Introduction

As a line is composed of an infinite number of points, confidence limits can be described by what is known as an epsilon (ε) or Perkal band at a fixed distance on either side of the line (Figure 1).

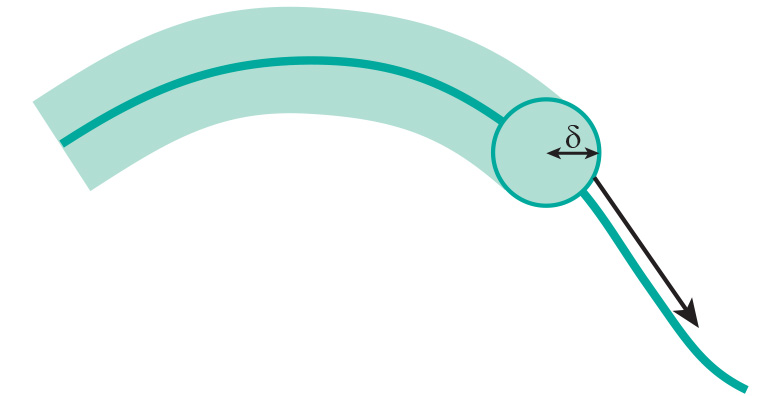
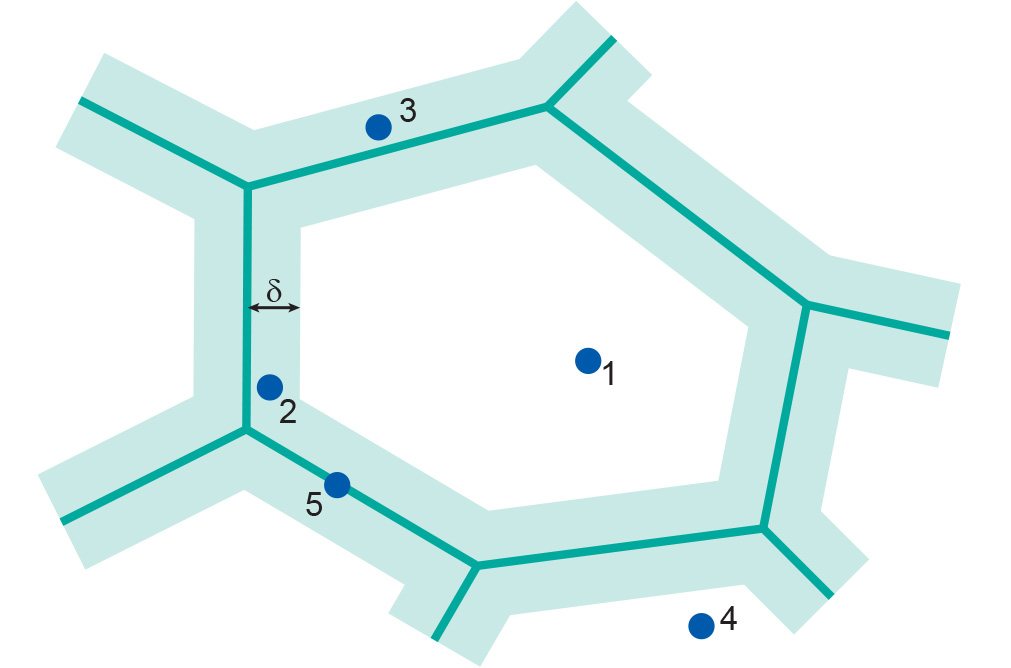
Figure 1: The ε or Perkal band is formed by rolling an imaginary circle of a given radius along a line.

The width of the band is based on an estimate of the probable location error of the line, for example to reflect the accuracy of manual digitizing. The epsilon band may be used as a simple means for assessing the likelihood that a point receives the correct attribute value (Figure 2).

Figure 2: The ε band may be used to assess the likelihood that a point falls within a particular polygon (source: Openshaw et al. (1991). Point 3 is less likely part of the middle polygon than point 2.

 

External resources

  • Openshaw, S., Charlton, M. & Carver, S. (1991). Error propagation: a Monte Carlo simulation. In I. Masser and M. Blakemore (Eds.). Handling geographical information: methodology and potential applications, pp. 78–101. Harlow, UK: Longman, Harlow.

Learning outcomes

Prior knowledge

Incoming relations