Membership functions

There are many situations, particularly in surveys of natural resources, where, according to Burrough and Frank (1996, p.16), “practical scientists, faced with the problem of dividing up undividable complex continua have often imposed their own crisp structures on the raw data”. In practice, the results of classification are normally combined with other categorical layers and continuous field data to identify, for example, areas suitable for a particular land use. In a GIS, this is normally achieved by overlaying the appropriate layers using logical operators.

Particularly in the case of natural resource maps, the boundaries between units may not actually exist as lines but only as transition zones, across which one area continuously merges into another. In these circumstances, rigid measures of positional accuracy, such as RMSE, may be virtually insignificant in comparison to the uncertainty inherent in vegetation and soil boundaries, for example.

In conventional applications of the error matrix to assess the quality of nominal (categorical) data such as land use, individual samples can be considered in terms of Boolean set theory. The Boolean membership function is binary, i.e. an element is either a member of the set (membership is true) or it is not a member of the set (membership is false). Such a membership notion is well-suited to the description of spatial features such as land parcels for which no ambiguity is involved and an individual ground truth sample can be judged to be either correct or incorrect. As Burrough and Frank (1996) note,

Since its original development by Zadeh (1965), there has been considerable discussion of fuzzy, or continuous, set theory as an approach for handling imprecise spatial data. In GIS, fuzzy set theory appears to have two particular benefits:

1. the ability to handle logical modelling (map overlay) operations on inexact data; and

2. the possibility of using a variety of natural language expressions to qualify uncertainty.

Unlike Boolean sets, fuzzy or continuous sets have a membership function, which can assign to a member any value between 0 and 1 (see Figure below). The membership function of the Boolean set of Figure a can be defined as MF^B, where:

The crisp and uncertain set membership functions of the Figure below are illustrated for the one-dimensional case. Obviously, in spatial applications of fuzzy set techniques we typically would use two-dimensional sets (and membership functions).

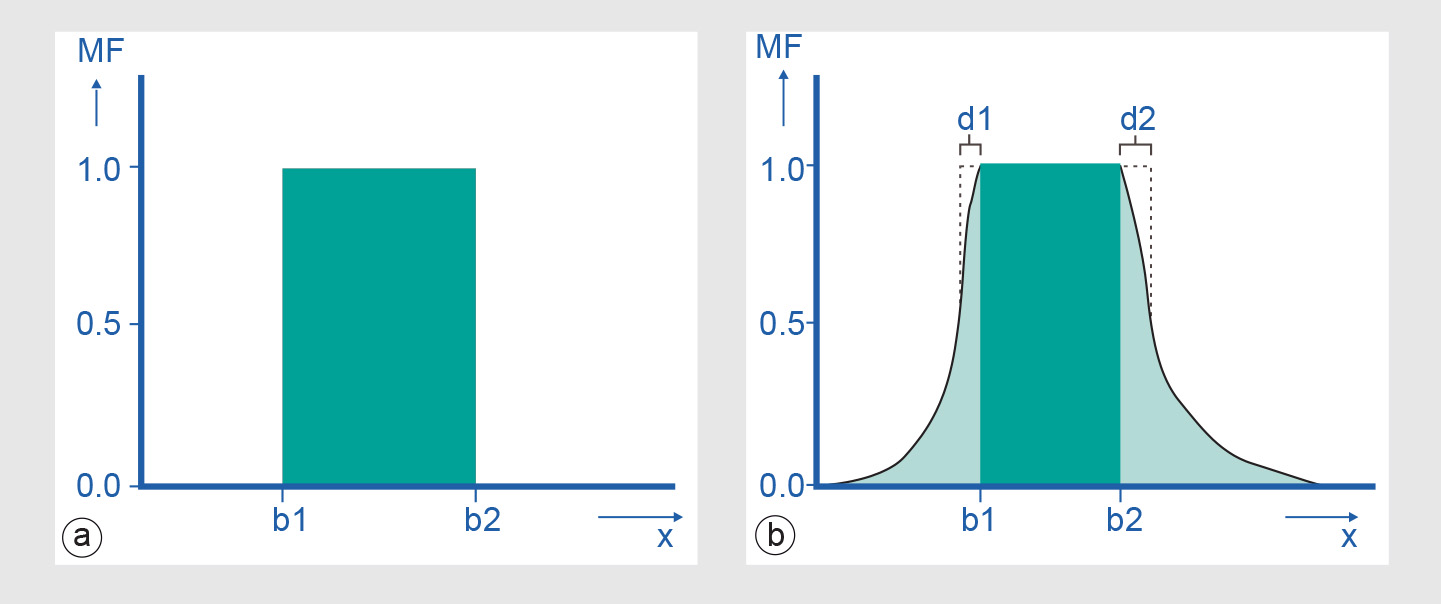
The continuous membership function of Figure b, in contrast to function MF^B above, can be defined according to Heuvelink (1993) as a function MF^C:

The parameters d₁ and d₂ denote the width of the transition zone around the kernel of the class such that MF^C(x) = 0.5  at the thresholds b₁ - d₁ and b₂ + d₂, respectively. If d₁ and d₂ are both zero, the function MF^C reduces to MF^B.

An advantage of fuzzy set theory is that it permits the use of natural language to describe uncertainty, for example, “near,” “east of” and “about 23 km from”. Such natural language expressions can be more faithfully represented by appropriately chosen membership functions.