Area representation

When area objects are stored using a vector approach, the usual technique is to apply a boundary model. This means that each area feature is represented by some arc/node structure that determines a polygon as the area’s boundary. A polygon representation for an area object is another example of a finite approximation of a phenomenon that may have a curvilinear boundary in reality.

Common sense dictates that area features of the same kind are best stored in a single data layer, represented by mutually non-overlapping polygons. This results in an application-determined (i.e. adaptive) partition of space. If the object has a fuzzy boundary, a polygon is an even worse approximation, even though potentially it may be the only one possible. The Figure illustrates a simple study with three area objects, each represented by polygon boundaries. Clearly, we expect additional data to accompany the area data. Such information could be stored in database tables.

A simple but naïve representation of area features would be to list for each polygon the list of lines that describes its boundary. Each line in the list would, as before, be a sequence that starts with a node and ends with one, possibly with vertices in between. A closer look at the shared boundary between the bottom left and right polygons in the Figure shows why this approach is far from optimal. As the same line makes up the boundary from the two polygons, this line would be stored twice in the above representation, namely once for each polygon. This is a form of data duplication—known as data redundancy—which is (at least in theory) unnecessary, although it remains a feature of some systems. Another disadvantage of such polygon-by-polygon representations is that if we want to identify the polygons that border the bottom left polygon, we have to do a complicated and time-consuming search analysis comparing the vertex lists of all boundary lines with that of the bottom left polygon. For the Figure above, with just three polygons, this is fine, but in a data set with 5000 polygons, and perhaps a total of 25,000 boundary lines, this becomes a tedious task, even with the fastest of computers.

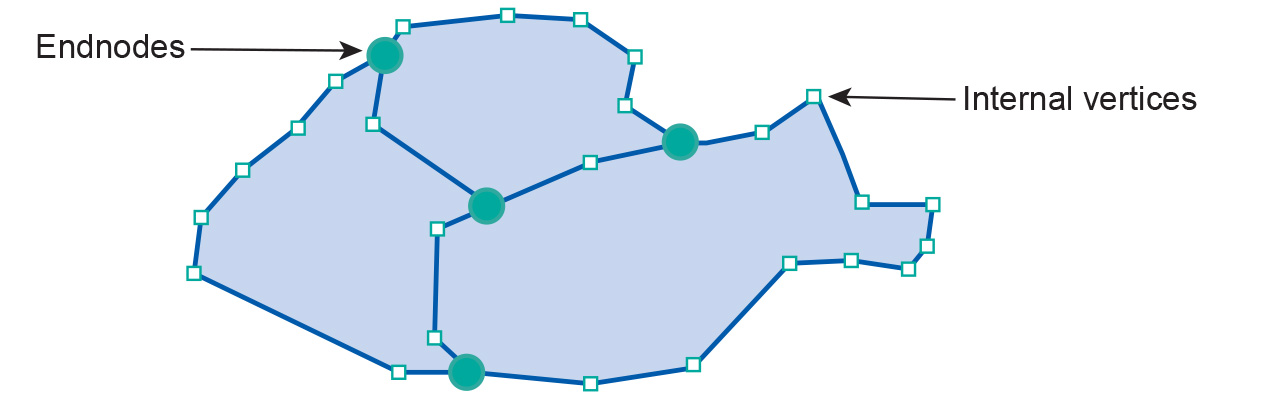
However, the boundary data model is an improved representation that deals with these disadvantages.