Model
Introduction
A model can be defined as a simplified representation of some aspects of a real system. By creating a model, we move from the real world into an abstract world of concepts, mathematical constructs, spatial queries and techniques for delivering solutions. We re-enter the real world with the solution in hand, at which stage that solution is translated into a useful answer to the real-world problem. Models - as simplified representations - come in many different "flavours".
Models can be used to serve various objectives or functions, for example to better understand a spatial phenomenon, to represent a phenomenon, to measure or calculate a distance, or to set up plans for a disaster response unit within a city.
Note that the models we build are defined by the purposes that they are to serve. If you only want your friend to get to your house, you will draw a very simple diagram, avoiding the description of various places of interest on her way. However, if you want her to take notice of a particular location, you might also show her a photograph, which is also a model. Its purpose is very different and so are the implementation, the scale, or the details.
Explanation
What is a model?
The word “model” can be read as a verb, which means “to describe” or “to represent”, but it can also be used as a noun. In Van Dale’s Dutch dictionary (Van Dale’s Groot Woordenboek der Nederlandse Taal) a “model” is defined as “a schematization of reality with operational potentials”. This points to the intimate relationship between the type and degree of schematization and the objectives for the call on the operational potentials. Meijer (1984) stresses this call on potentials as follows: “A model is an object or concept that is used to represent something else. It is reality scaled down and converted to a form we can comprehend.”
Here we will use the following definition of a model: “A model is a manageable, comprehensible and schematic representation of a piece of reality”. This definition can be explained as follows:
-
“reality”: as scientists we usually wish to model reality and not a hypothetical system. Reality is, however, vast and infinitely complex. Describing (modelling) reality in all its facets and complexity is therefore impossible.
-
“a piece of reality”: we focus on a limited domain in time and space, incorporating only specific aspects, focusing on perhaps only one or just a few objectives. We represent a number of phenomena that we can observe in reality, usually to enable study, administration, computation and/or simulation.
-
“schematic representation”: reality is only considered from a specific point of view. This implies imperfections and limited accuracy (e.g. projection of the Earth onto a map).
-
“representation”: an infinite number of projections, thus different representations of the same piece of reality are possible, resulting in an equal number of modelling possibilities.
-
“a comprehensible representation”: a model serves a specific goal. A model is used as an aid to diagnose, analyse or predict the behaviour of the modelled system. The user is central in this. The user needs to be able to understand the functioning of the model itself, as well as how the model and the real world differ.
-
“a manageable representation”: for the same reason as the previous item, the model needs to be manageable. It should give users the results they need to be able to answer their questions, to find solutions to their problems. Users need to be able to “play” with the model (change variables, experiment, evaluate, etc.)
Model Characteristics
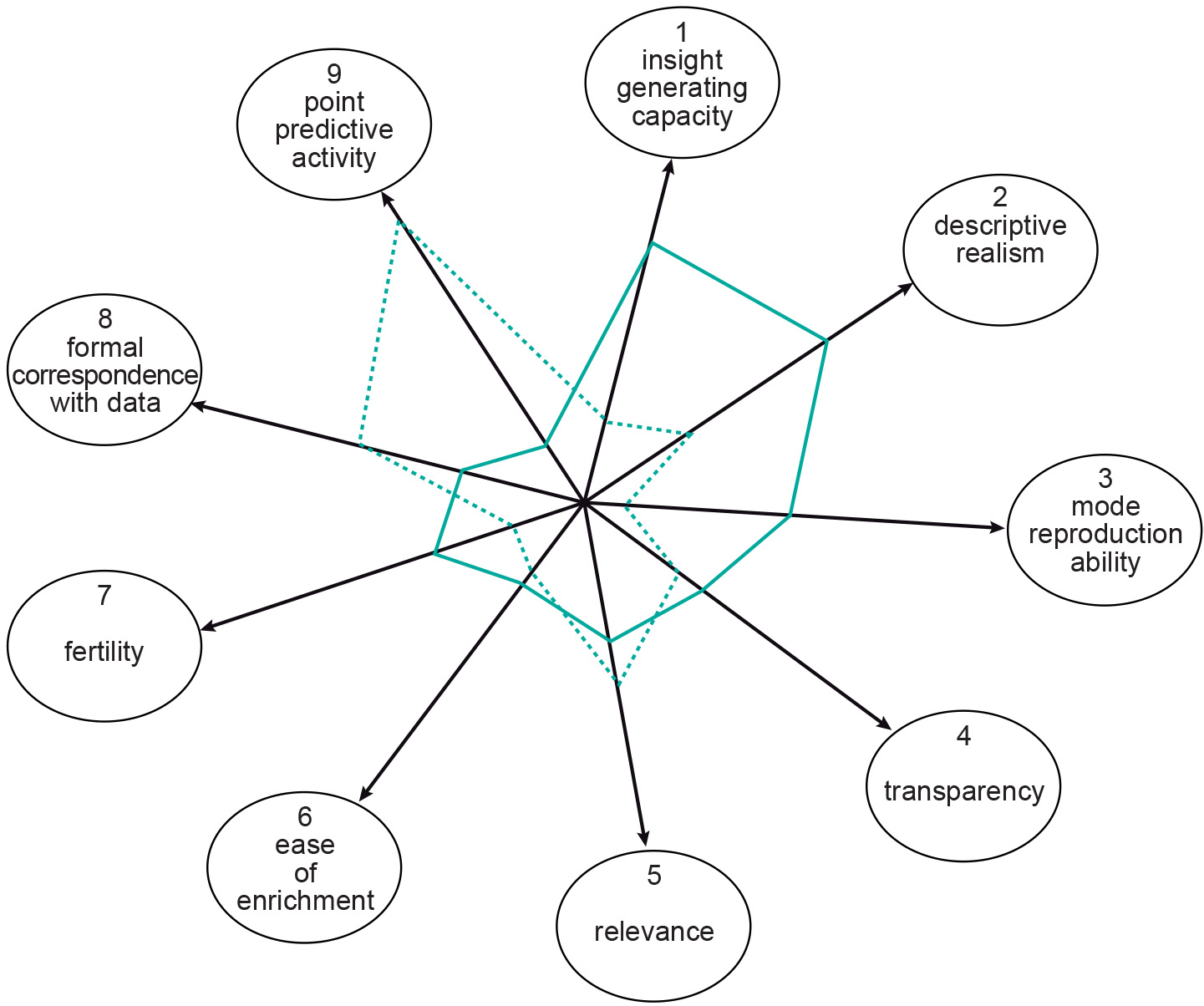
Randers (1980) distinguished nine general characteristics of models, where the objective of the study determines the importance of each of the characteristics. These general characteristics are:
-
insight-generating capacity: the model increases insight into the system and its image;
-
descriptive realism: system and model structure are similar;
-
model reproduction ability: model reproduces typical system behaviour;
-
transparency: the model is useable and understandable, also by non-experts;
-
relevance: according to experts, the model provides meaningful solutions to the problem;
-
ease of enrichment: the model can easily be adapted;
-
fertility: the model stimulates generation of new ideas, new experiments, new policy;
-
formal correspondence with data: the model reproduces known observations accurately;
-
point predictive ability: the model makes good predictions.
Most models, particularly those used in GI Science, try to increase knowledge of and insight into the observed behaviour of systems or to estimate the effect of changes (choice options) on their behaviour.
Examples
In the GIS environment, the most familiar model is a map. A map is a miniature representation of a part of the real world. Databases are another important class of models. A database contains (spatial) data and also provides various functions for operating on that data. The collection of stored data represents a real-world phenomena, so it also is a model. Digital models (such as a database or GISs) have advantages over paper models (e.g. analogue maps), being more flexible and therefore more adaptable for the purpose at hand. Digital models may also allow animations and simulations.
“Data modelling” is the common name for the design effort of structuring a database. It involves the identification of the kinds of data that the database will store and the relationships between them. Most maps and databases can be considered static models, representing a single state of affairs at a point in time. Dynamic models or process models, on the other hand, address developments or changes in the real world: changes in the past, in the present or at sometime in the future. Dynamic models are inherently more complicated than static models and usually require much more computation. Simulation models are an important class of dynamic models that allow the simulation of real-world processes.
GISs and application models We have already mentioned that real-world processes are often highly complex. Models are simplified abstractions of reality representing or describing its most important elements and their interactions. Modelling and GISs are connected, since a GIS is itself a tool for modelling a part of “the real world”. The solution to a problem usually depends on a number of parameters. Since these parameters are often interrelated, their interaction is made more precise in an application model. Such a model describes as faithfully as possible how the relevant phenomena (in our case, often geographic) behave, doing so in terms of the parameters
External resources
- Randers, J. (1980). Guidelines for Model Conceptualization. In J. Randers (Ed.). Elements of the System Dynamics Method. Waltham, MA : Pegasus Communications.
Outgoing relations
- Model is based on Data
- Model is produced by Modelling
- Model is used by Spatial data acquisition
Incoming relations
- Map is a kind of Model
- Process model is a kind of Model
- Systems model is a kind of Model