Map projection equations

In creating the mathematical basis of a map, it is necessary to construct a network of meridians and parallels or some other coordinate lines in the selected projection, which serve as a skeleton for entering other content. The graphic way of constructing these cartographic networks initially fully met the requirements of geography and cartography. Over time, since the basic points were determined by triangulation, and the maps were drawn based on topographic surveying, it was necessary to draw cartographic networks more accurately, which could be achieved by calculating the numerical values of the coordinates of the points along the meridian and parallels in the projection. We call this method analytical, because the coordinates should be expressed using mathematical formulas, i.e. in analytical form. Therefore, for each map projection, it is necessary to establish a functional connection between points on the surface of the sphere or ellipsoid and in the plane of the projection. This functional dependence is expressed by basic cartographic equations.

In the selected projection, it is necessary to construct a network of meridians and parallels and draw other content depending on the purpose of the map. Map projection is most often given analytically by the basic cartographic equations:   where x and y are functions of the geographic or geodetic coordinates φ and λ, while numerical values of x and y are rectangular coordinates in the projection plane. Sometimes it is more convenient to use the polar coordinate system. Then the basic cartographic equations have this form: ,where ρ and δ are functions of the geographic or geodetic coordinates φ and λ, while numerical values of ρ and δ are polar coordinates in the projection plane. Sometimes we need a reverse link. Then the inverse cartographic equations or the inverse functions have this form: , or . We use appropriate software to apply cartographic equations. Equations of different map projections can be found in the literature (e.g. Snyder 1987, Snyder and Voxland 1989) and on the Internet (e.g. https://proj.org/). The representation of a curved surface in any projection in a plane is distorted. Distances, areas, and angles are changed or deformed during mapping. Distortion sizes are one of the important indicators of the value of the map projection.

The Sinusoidal Pseudocylindrical projection (Fig. 1) was developed in the 16th century and used by J. Cossin in 1570 and by J. Hondius in Mercator atlases of the early 17th century. It is often called the Sanson-Flamsteed projection after later users.

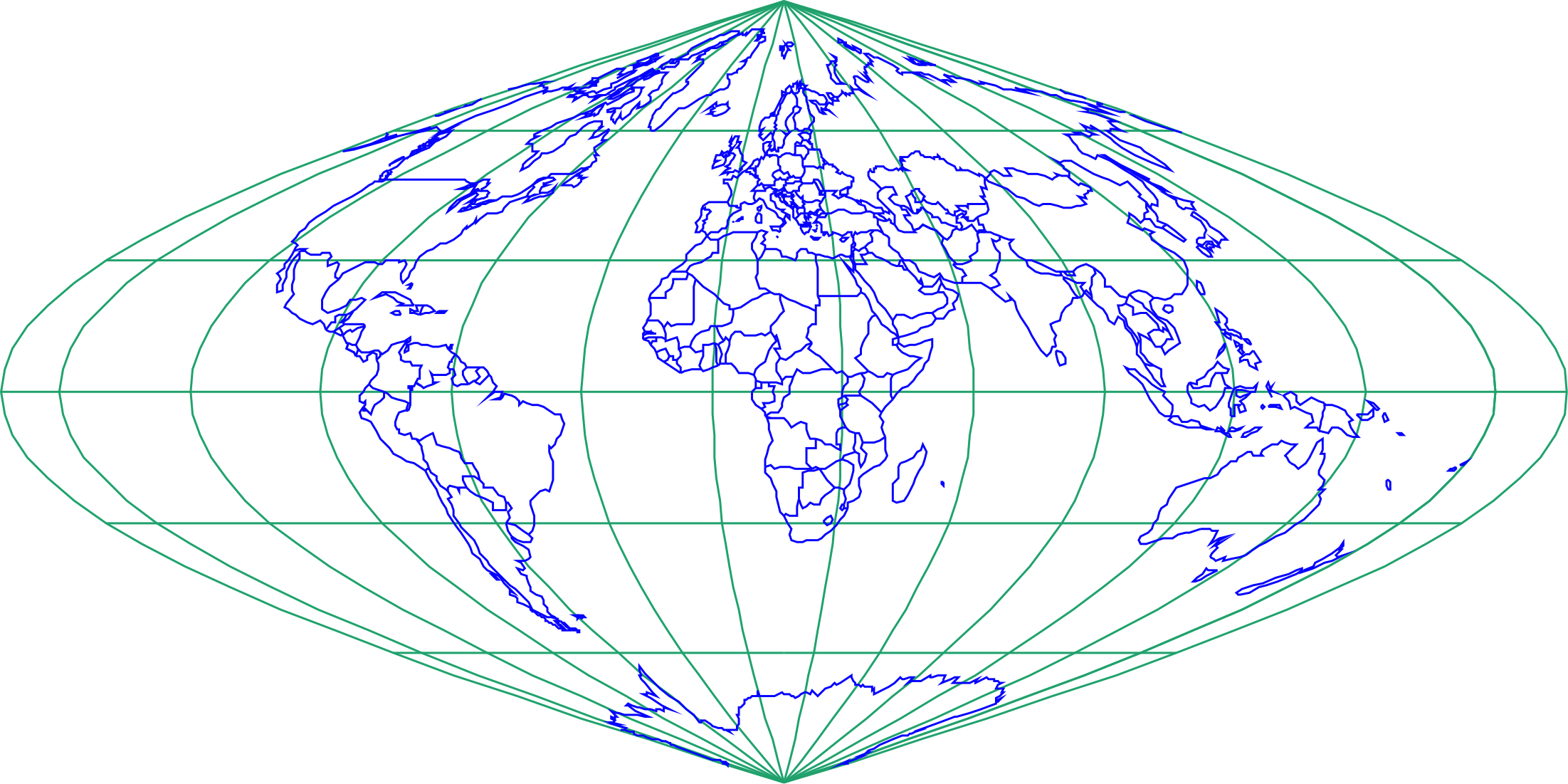
Figure 1: World map in the Sinusoidal Pseudocylindrical projection with

The equations of the Sinusoidal pseudocylindrical projection are: where R is the Earth radius, φ and λ are the geographic latitude and longitude, respectively, and is the longitude of the central meridian and a constant of the projection. x and y are rectangular coordinates in the plane of projection. Inverse equations of the Sinusoidal Pseudocylindrical projection are: . The Equidistant conic projection (Fig. 2) in rudimentary forms was developed by Claudius Ptolemy (about A. D. 100). It is also known as the Simple Conic projection.

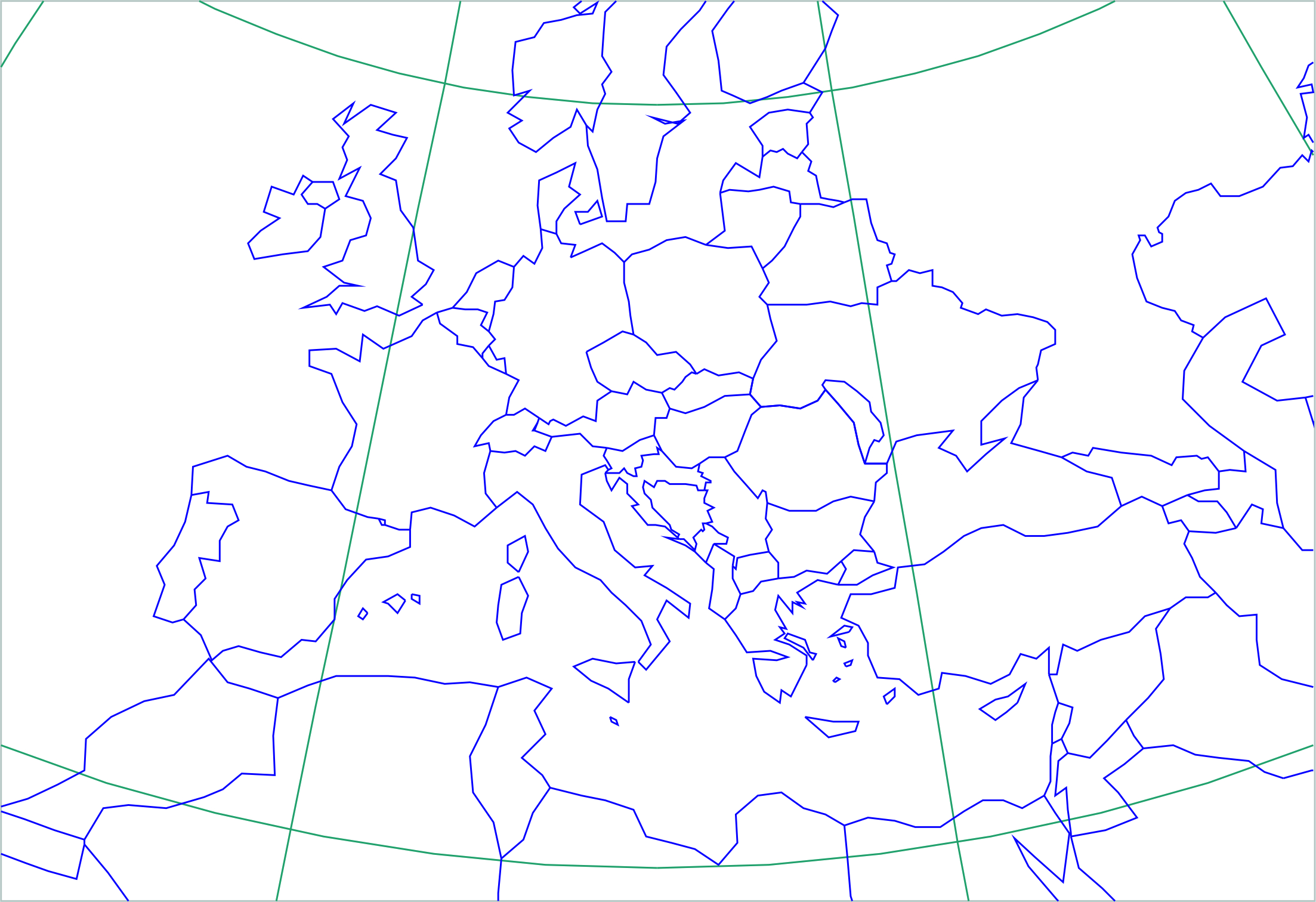
Figure 2: Part of Europe in the Equidistant Conic projection, with  and standard parallels be  and .

The equations of this projection are: where R is the Earth radius, φ and λ are geographic latitude and longitude, respectively, is the longitude of the central meridian, are two given latitudes, known as latitudes of standard parallels, , , and ρ and δ are polar coordinates in the plane of projection. Inverse equations of the Equidistant Conic projection are: .

Let us suppose that the latitude of a point is φ = 45.80984 N and longitude λ = 15.95169 E. The radius R of the Earth is 6370 km, and the longitude of the central meridian E. Rectangular coordinates in the plane of the Sinusoidal Pseudocylindrical projection of the given point will be  , The values for x and y are expressed in kilometres because the Earth's radius is given in kilometres. If necessary, kilometres can be converted to other units of length. For displaying on the map, it is necessary to consider the scale of the map. Let us suppose that the latitude of a point is φ = 45.80984 N and longitude λ = 15.95169 E. The radius R of the Earth is 6370 km, and the longitude of the central meridian E. To compute the polar coordinates in the plane of the Equidistant Conic projection of that point we need two more constants: and  , two given latitudes. Let them be N and N. Now, we are able to calculate two constants: , .  Polar coordinates in the plane of the Equidistant Conic projection will be: . The value of ρ is expressed in kilometres because the Earth's radius is given in kilometres. The value of δ is expressed in degrees. If necessary, kilometres can be converted to other length units, and degrees to radians. For displaying on the map, it is necessary to consider the scale of the map.