Map projection, classification

There is an infinite number of different map projections, and several hundred are known. To make them easier to study and therefore select for practical application, we divide them into groups.
As a basis for the division of map projections are usually taken:
1. Properties of mapping or types of distortions
2. The shape of a (pseudo)graticule
3. Projection aspect, i.e., position of the axis of projection in relation to the axis of rotation of the sphere.

Classification of Map Projections According to Types of Distortions
According to the types of distortions, map projections can be divided into these four groups: conformal (equiangular), equivalent (equal-area), equidistant in a certain direction (equal-length) and compromise. Let us define the local linear scale factor c = ds'/ds, where ds' is a differential of arc length in the plane of projection, and ds is the appropriate differential of arc length on the original surface, usually a sphere or ellipsoid. Analogously, the local area scale factor p = dp'/dp, where dp' is a differential of an area in the plane of projection and dp is the appropriate differential of the area on the original surface.
In conformal projections, the distortion of the angles is equal to zero, and the linear scale factor at a point is equal in all directions, i.e., it does not depend on the azimuth. Because angle distortion in the conformal projections is zero and the scale does not depend on the azimuth at each point, the similarity of the corresponding infinitesimal figures on the ellipsoid and in the plane is preserved, hence their name conformal, i.e., similar in form.
In equal-area projections, the equality of the area of the corresponding figures on the ellipsoid and in the projection is preserved. Therefore, in equal-area projections, the local area scale factor is equal to one in the entire map field.
In equidistant projections, the local linear scale factor is equal to one along one of the main directions, i.e., the directions along which the linear scale factor has the largest and smallest value. Equidistant projections are in the middle between conformal and equal-area projections by types and magnitudes of distortions. Namely, in equidistant projections, area distortions are smaller than in conformal projections, and angle distortions are smaller than in equal-area projections.
The group of compromise projections includes all those projections that are neither conformal, equivalent, nor equidistant.

Classification of Projections According to the Shape of the Pseudograticule
The network of pseudomeridians and pseudoparallels (pseudograticule) is obtained by rotating the network of meridians and parallels (graticule) to any other position (Fig. 1 and 2).

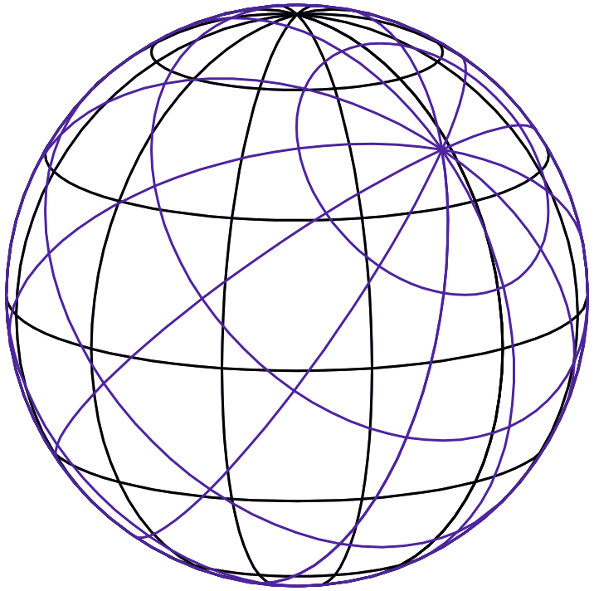
Figure 1: Graticule (black) and pseudograticule (blue) on a sphere.

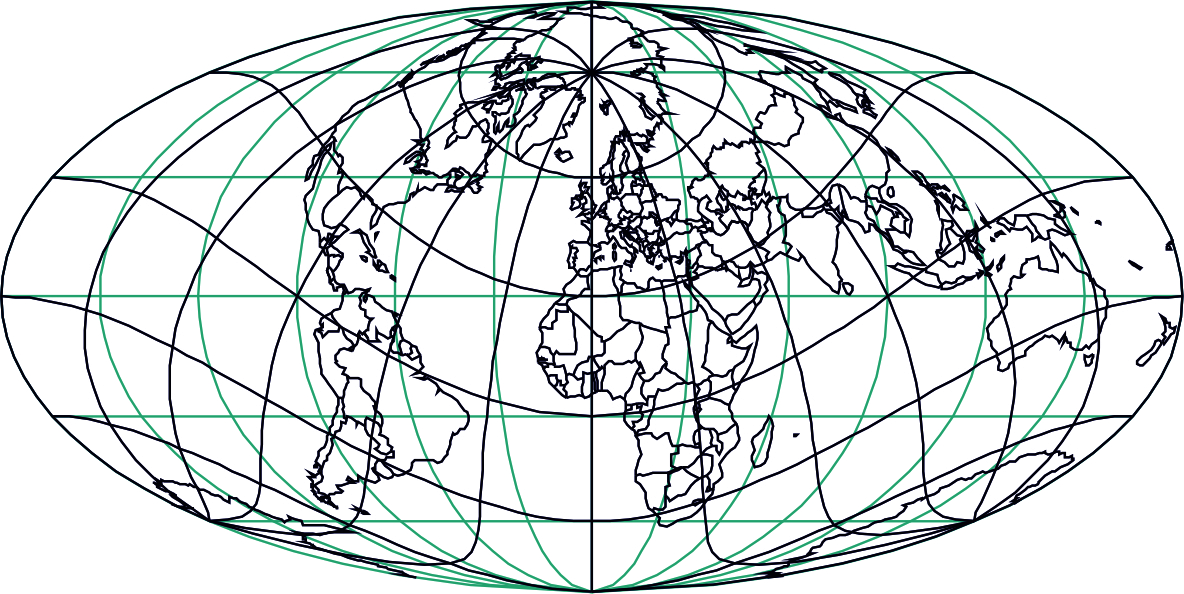
Figure 2: Image of the graticule (black) and the pseudograticule (blue) in the oblique Mollweide projection.

It is obvious that if there is no mentioned rotation, then the pseudograticule coincides with the graticule.
The pseudograticule has the important property that, regardless of the aspect of the projection, it retains the characteristic shape for a particular group of projections and thus allows a unique definition of each group of projections.

Classification of Projections According to the Aspect of Projection
The classification of projections according to the position of the axis of projection in relation to the axis of rotation of the sphere is applied primarily to the mapping of the sphere. The straight line passing through the poles of the pseudograticule is the axis of projection. The position of the axis of the projection in relation to the axis of rotation of the sphere parameterized by geographical parameterization is called the aspect of the projection. The aspect can be normal, transverse, or oblique.

Example of map projections classification according to types of distortions
Conformal: Mercator projection, Gauss-Krüger projection, Lambert conformal conic projection
Equal-area: Mollweide projection, Albers Equal-Area Conic projection, Eckert IV projection
Equidistant: Cassini projection, Plate Carree, Azimuthal Equidistant projection

Example of map projections classification with different shape of pseudograticule

• Cylindrical projections are projections in which pseudomeridians are shown in mutually parallel straight lines and pseudoparallels in mutually parallel straight lines perpendicular to images of pseudomeridians (Figure 3a). Cylindrical projections are not mappings onto a cylindrical surface in general. A map made in a cylindrical projection can be folded into a cylindrical surface.
• Conic projections in the narrower sense are projections in which pseudomeridians are represented by straight lines that intersect at one point and pseudoparallels by concentric circular arcs, with the angle between any two pseudomeridians being less than the difference of the corresponding pseudogeographic longitudes (Figure 3b). Conic projections are not mappings onto a conical surface in general. A map made in a conic projection can be folded into a conical surface.
• Azimuthal projections are projections in which pseudomeridians are shown as straight lines that intersect at one point and pseudoparallels by concentric circles, with the angle between any two pseudomeridians being equal to the difference of the corresponding pseudogeographic longitudes (Figure 3c). Azimuthal projections are planar projections, but this is not their special characteristic because all map projections are mappings onto a plane.
• Pseudocylindrical projections are projections in which pseudomeridians are represented by curves symmetrical with respect to the middle pseudomeridian mapped as a straight line and pseudoparallels as mutually parallel straight lines perpendicular to the image of the central pseudomeridian (Figure 3d).
• Pseudoconic projections are projections in which pseudomeridians are represented by curves symmetric with respect to the middle pseudomeridian mapped as a straight line and pseudoparallels as arcs of concentric circles (Figure 3e).
• Polyconic projections are projections in which pseudomeridians are mapped as curves symmetric with respect to the central pseudomeridian which is mapped as a straight line, and pseudoparallels are mapped as eccentric circles whose centers are on the central pseudomeridian (Figure 3f).
• Circular projections are projections in which pseudomeridians are mapped as arcs of circles symmetrical in relation to the central pseudomeridian which is mapped as a straight line, and pseudoparallels are mapped as arcs of circles whose centers are on the central pseudomeridian (Figure 3g).
• Other projections are projections in which pseudomeridians and pseudoparallels are mapped as more complex curves (Figure 3h).

Figure 3: Classification of projections according to the shape of the pseudograticule: (a) cylindrical; (b) conic; (c) azimuthal; (d) pseudocylindrical; (e) pseudoconic; (f) polyconic; (g) circular; (h) other.
 

Example of map projections classification according to the aspect of projection
Mollweide projection in normal, transverse and oblique aspect (Fig. 4).

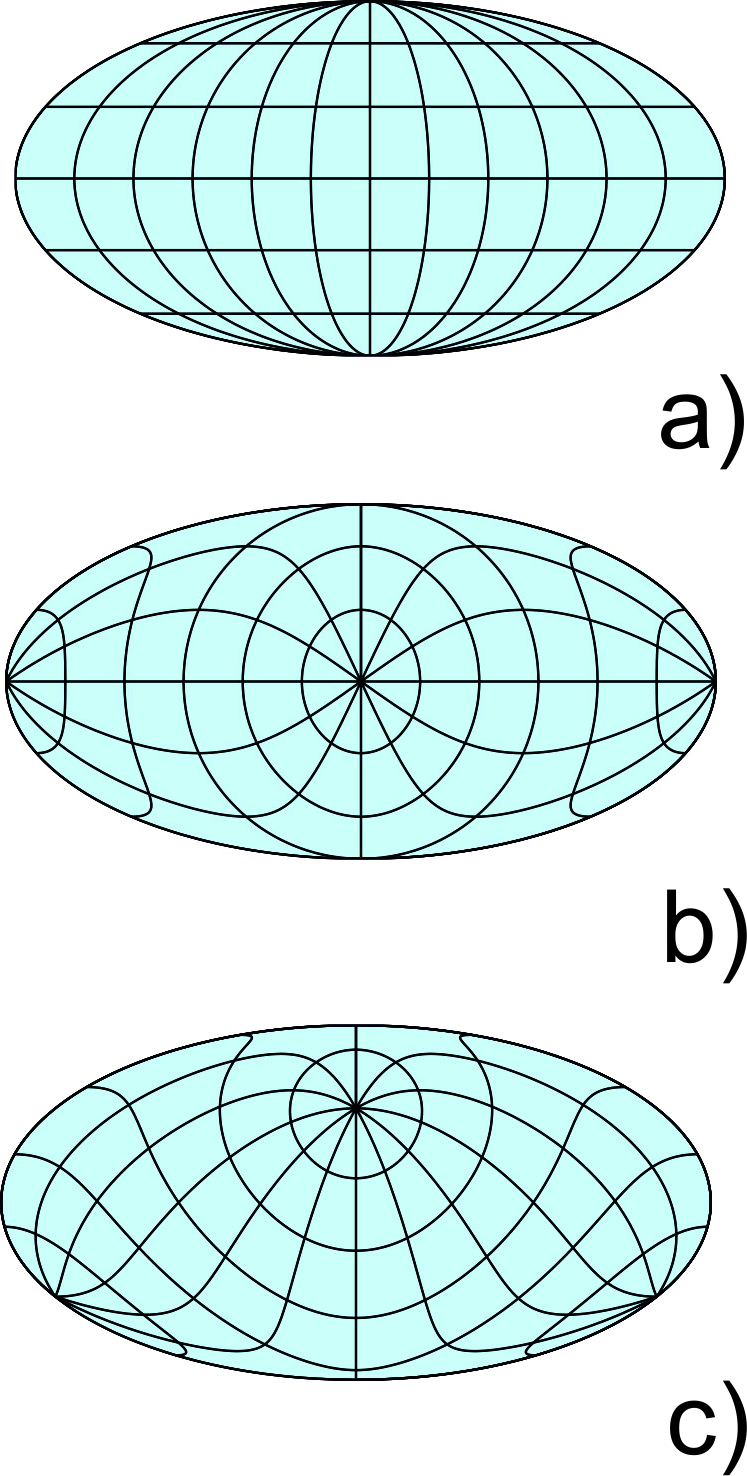
Figure 4: Image of the graticule in the Mollweide (a) normal aspect projection, (b) transverse aspect projection, (c) oblique aspect projection.

To make map projections easier to study and therefore select for practical application, they are divided into groups. Some specific criteria that affect the appropriate selection of a projection are the size and location of the region to be mapped; specific properties of the projection to be maintained, such as conformality, equivalence of areas, and equivalence of distances; specific characteristics, such as constant scale along the Equator or along a meridian or centred on a specific location.

List basic classes of map projections.
What are conformal projections?
What are equal-area projections?
What is the basic property of equidistant projections?
How are the projections divided according to the shape of the normal graticule?
How are projections divided in relation to aspect?