Term map projection

The name ‘map projection’ contains the word ‘projection’. Obviously the problem may arise in that word, which has a number of meanings, as is evident if we peek into any dictionary. That means that the term ‘map projection’ is rather awkward, as it can lead the uninitiated to the wrong conclusion that it is the result of geometrical projection, rather than a special type of mapping that includes three notions: the area of definition or domain, mapping law, and the area of value or codomain.

In mathematics, mapping one surface onto another means establishing correspondence between the points of the two surfaces. In our field of interest, any method of mapping all or part of the surface (usually of the Earth's ellipsoid or the Earth's sphere) into a plane is called a map projection.

The law that connects the position of a point on the surface with the position of the image of that point on the plane – on the map – can be often expressed mathematicaly (geometrically or analytically). The analytical expression of the mapping law is achieved by a system of equations that allow the use of the coordinates (for example, the latitude and longitude) of the mapped point to calculate the coordinates of its image (for example, planar rectangular or polar).
In geometry, the word ‘projection’ means either an orthogonal projection, in which the simplest technical drawings are made, or a perspective that is more general.

The term ‘map projection’ entered cartography from mathematics, but it does not refer only to projections known in mathematics, such as perspective or central projection and axonometry, or parallel projection. The noun ‘projection’ in cartography should be understood conditionally, as it refers to any mapping of a curved surface, most commonly a sphere or ellipsoid, into a plane.

The two well-known and very useful projections for limited areas, the Gnomonic and Stereographic, are derived directly from the perspective model, but most projections are produced mathematically.
Let us consider the general perspective view of the globe (Figure 1).

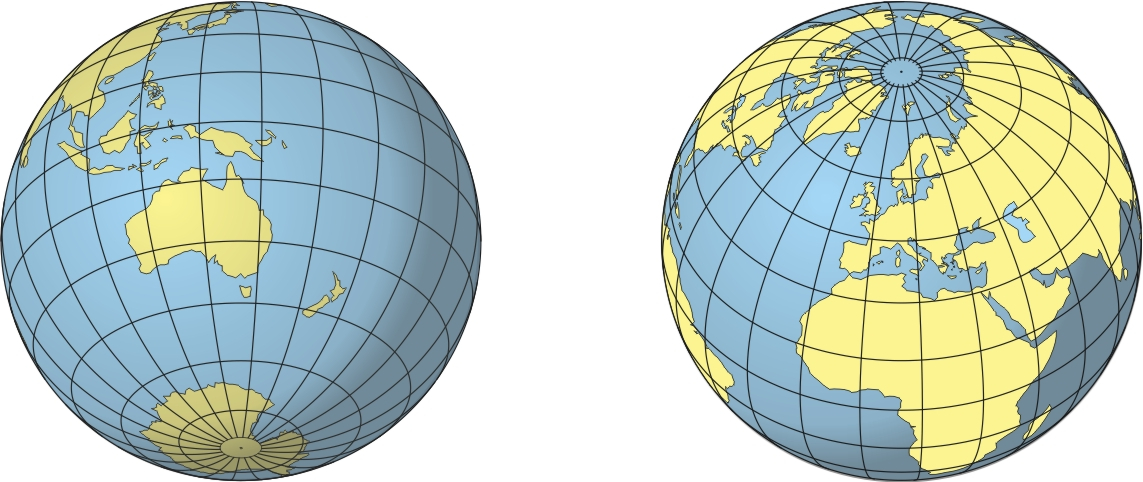
Figure 1: Two globe hemispheres in perspective projection

The Orthographic is a view from an infinite distance, but by bringing in the viewpoint to a few thousand or a few hundred kilometers from the surface of the Earth, we can get other perspectives, like that of a camera viewing Earth from space. When astronauts photographed portions of the Earth during the Apollo and Gemini missions, they were in effect using a tilted form of a perspective projection, with the regions that surround the points of interest fading into the horizon.
There are many non-perspective map projections (Figures 2 – 5). E.g. the Eckert projections are six pseudocylindrical map projections devised by Max Eckert-Greifendorff, who presented them in 1906. The latitudes are parallel lines in all six projections. The projections come in pairs; in the odd-numbered projections, the latitudes are equally spaced, while their even-numbered counterparts are equal-area. The three pairs are distinguished by the shapes of the meridians. Eckert I and Eckert II have rectilinear (straight-line) meridians, meeting at the equator at an angle. In Eckert III and Eckert IV (Figure 2), meridians are elliptical, while in Eckert V and Eckert VI, they are sinusoidal.

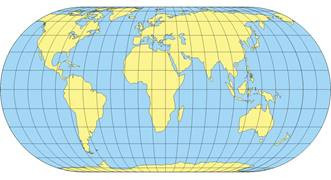
Figure 2: The earth on an Eckert IV equal-area projection

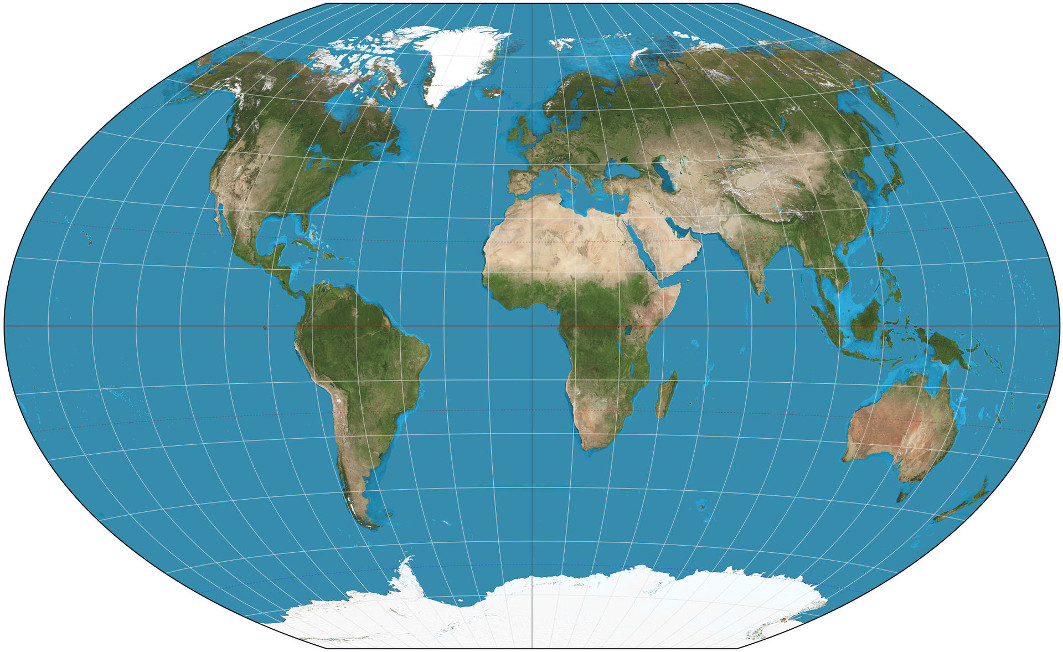
Figure 3: The Winkel Triple projection

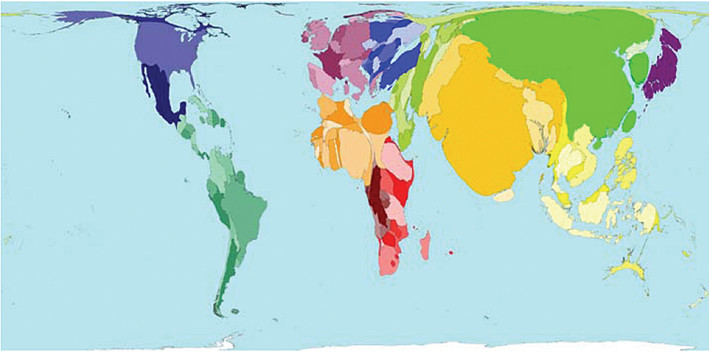
Figure 4: Equal world population projection, Dorling et al. 2008

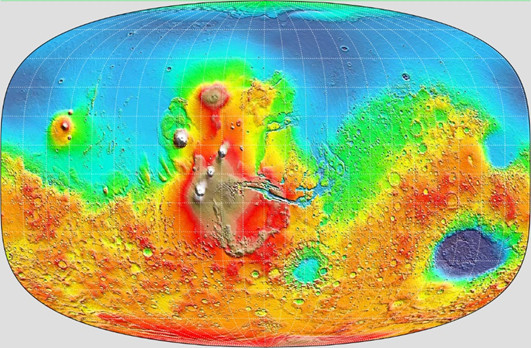
Figure 5: Map of Mars produced using Györffy A Projection

The term ‘map projection’ in cartography should be understood conditionally, as it refers to any mapping of a curved surface, most commonly a sphere or ellipsoid, into a plane.

How do the terms of projections in mathematics and technology differ from the same name in cartography?