Thiessen Polygons

Thiessen polygon partitions make use of geometric distance to determine neighbourhoods.

This is useful if we have a spatially distributed set of points as target locations and we want to know the closest target for each location in the study. This technique will generate a polygon around each target location that identifies all those locations that “belong to” that target.

We can see the use of Thiessen polygons in the context of interpolation of point data. Given an input point set that will be the polygon’s midpoints, it is not difficult to construct such a partition. It is even much easier to construct if we already have a Delaunay triangulation for the same input point set.

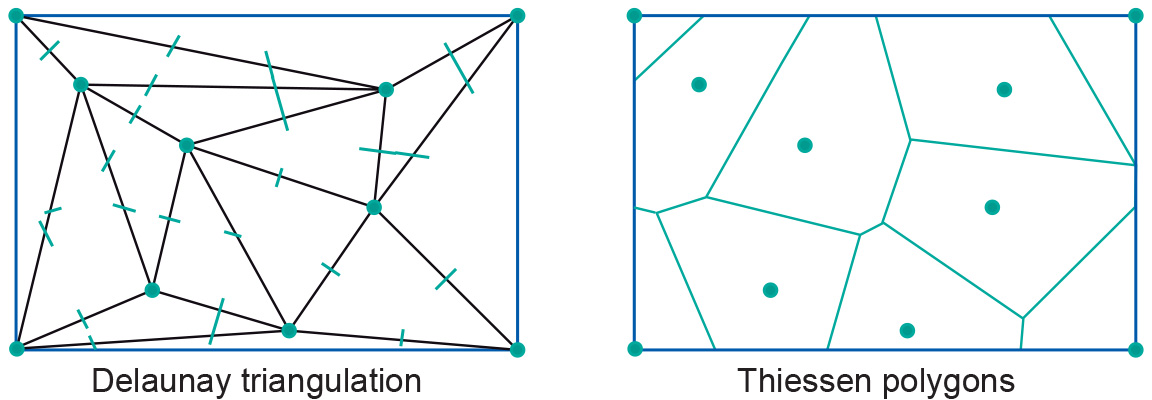
Left side of the Figure above shows the Delaunay triangulation; the Thiessen polygon partition constructed from it is on the right. The construction first creates the perpendiculars of all the triangle sides; note that a perpendicular of the side of a triangle that connects point A with point B is the imaginary line dividing the area between the area closer to A and the area closer to B. The perpendiculars become part of the boundary of each Thiessen polygon computed by the GIS. (The GIS will work for higher-precision real arithmetic rather than for what is illustrated here.)