Open map List

Vector Measurements

Introduction

The primitives of vector data sets are the point, (poly)line and polygon. Related geometric measurements are location, length, distance and area size. Some of these are geometric properties of a feature in isolation (location, length, area size); others (distance) require two features to be identified.

Explanation

Location Measurement

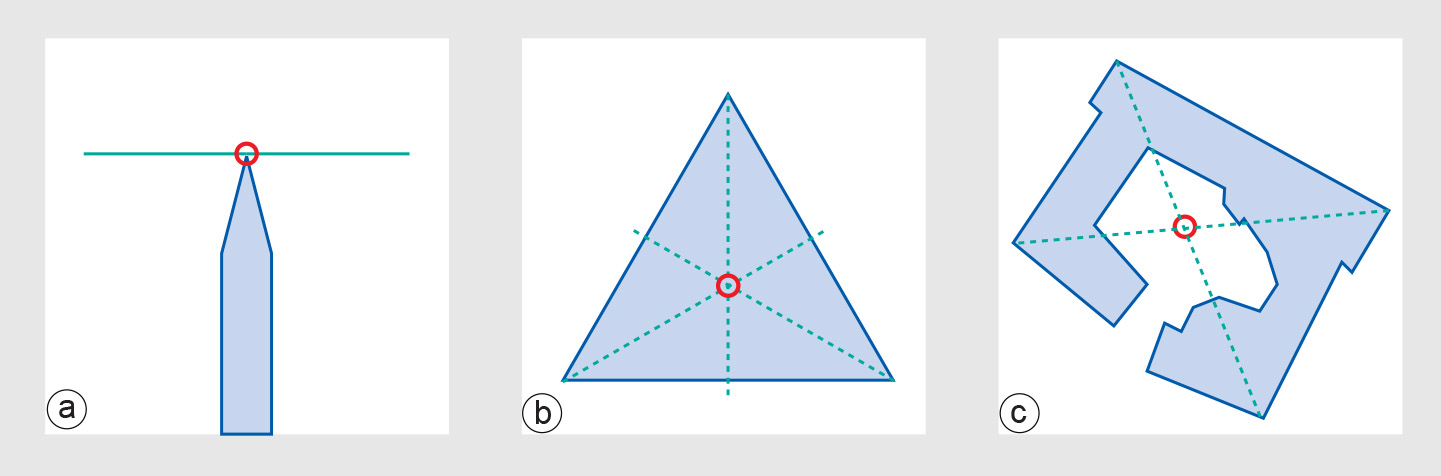
The location property of a vector feature is always stored by the GIS: a single coordinate pair for a point, or a list of pairs for a polyline or polygon boundary. Occasionally, there is a need to obtain the location of the centroid of a polygon (Figure 1); some GISs store these also, while others compute them on the fly.

Figure 1: The centroid: (a) the centroid of an object can be visualized as the point on which the object would balance when placed on the tip of a pencil, (b) the centroid of a polygon, (c) the centroid of the ITC building is actually outside the building (in the courtyard).

Length Measurement

Length is a geometric property associated with polylines, by themselves or in their function as polygon boundaries. It can obviously be computed by the GIS - as the sum of lengths of the constituent line segments - but quite often it is also stored with the polyline.

Distance Measurement

Measurement of distance between two features is another important function. If both features are points, say p and q, the computation in a Cartesian spatial reference system is given by the well-known Pythagorean distance function:

dist(p%2C%5C%2Cq)%3D%5Csqrt%7B(x_p-x_q)%5E2%2B(y_p-y_q)%5E2%7D
Equation 1

If one of the features is not a point, or both are not, we must be precise in defining what we mean by their distance. All these cases can be summarized as computation of the minimal distance between a location occupied by the first feature and a location occupied by the second feature. This means that features that intersect or meet, or when one contains the other, have a distance of 0. We leave a further case analysis, including polylines and polygons, to the reader as an exercise. It is not possible to store all distance values for all possible combinations of two features in any reasonably-sized spatial database. As a result, the system must compute on-the-fly whenever a distance computation request is made.

Area Size Measurement

Area size is associated with polygon features. Again, it can be computed, but it is usually stored with the polygon as an extra attribute value. This speeds up the computation of other functions that require area size values. The attentive reader will have noted that all of the above “measurements” do not actually require computation but only retrieval of stored data.

A common use of area size measurements is when one wants to sum up the area sizes of all polygons belonging to some class. This class could be crop type: what is the size of the area covered by potatoes? If our crop classification is in a stored data layer, the computation would include (a) selecting the potato areas, and (b) summing up their (stored) area sizes. Clearly, little geometric computation is required in the case of stored features. This is not the case when we are interactively defining our vector features for GIS use and we want measurements to be performed on these interactively defined features. Then the GIS will have to perform complicated geometric computations.

Minimal Bounding Box

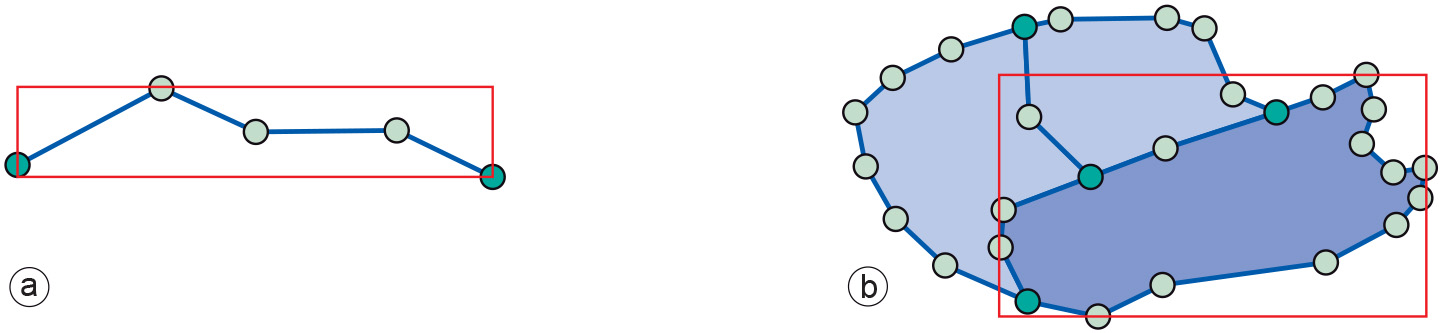
Another geometric measurement used by GISs is the minimal bounding box computation (Figure 2). It applies to polylines and polygons and determines the minimal rectangle - with sides parallel to the axes of the spatial reference system - that covers the feature.

Figure 2: The minimal bounding box of (a) a polyline, and (b) a polygon

Learning outcomes

  • 11 - Spatial analysis: classes of functions

    Classify and explain spatial analysis functions (measurements, classification, overlay, neighbourhood and connectivity) in a raster and vector environment (level 1 and 2).

Prior knowledge

Outgoing relations

Learning paths