Absolute positioning

The working principles of absolute, satellite-based positioning are fairly simple:

1. A satellite, equipped with a clock, sends a radio message at a specific moment that includes

   1. the satellite identifier,

   2. its position in orbit, and

   3. its clock reading.

2. A receiver on or above the planet, also equipped with a clock, receives the message slightly later and reads its own clock.

3. From the time delay observed between the two clock readings, and knowing the speed of radio transmission through the medium between (satellite) sender and receiver, the receiver can compute the distance to the sender, also known as the satellite’s pseudorange. This pseudorange is the apparent distance from satellite to receiver, computed from the time delay with which its radio signal is received.

Such a computation places the position of the receiver on a sphere of radius equal to the computed pseudorange (see Figure 1). If, instantaneously, the receiver were to do the same with a message from another satellite positioned elsewhere, the position of the receiver would be placed on another sphere. The intersection of the two spheres, which have different centres, describes a circle as being the set of possible positions of the receiver. If a third satellite message is taken into consideration, the three spheres intersect at, at most, two positions, one of which is the actual position of the receiver. In most, if not all practical situations where two positions result, one of them is a highly unlikely position for a signal receiver, thus narrowing down the true position of the receiver. The overall procedure is known as trilateration: the determination of a position based on three distances.

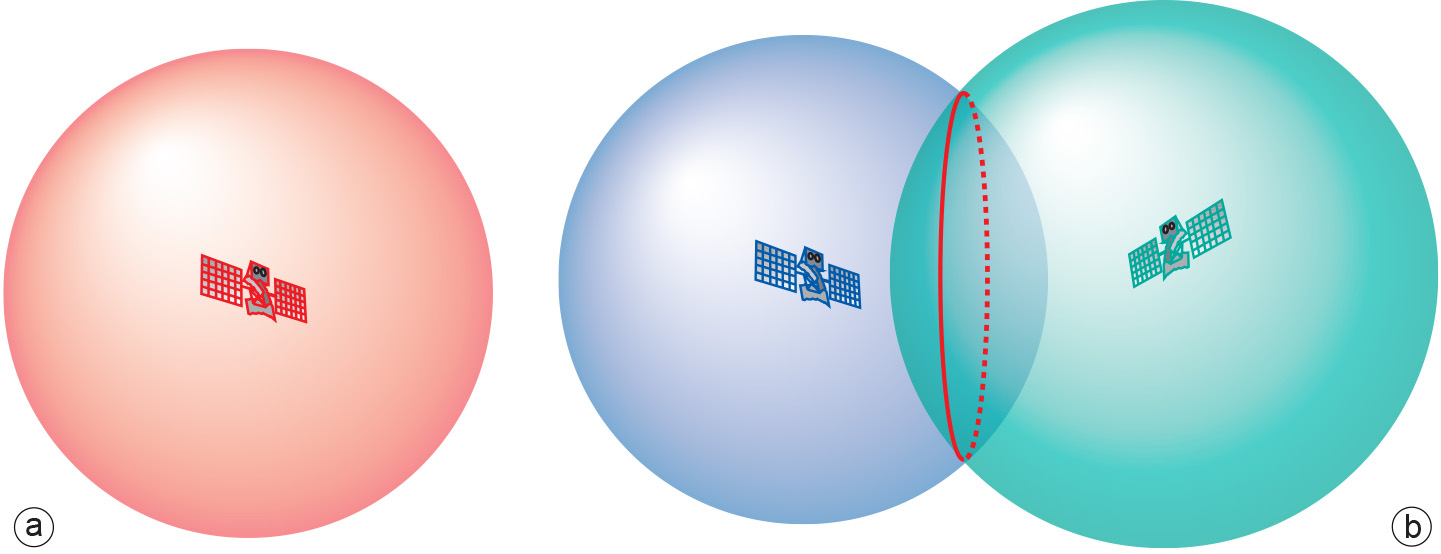
It would appear, therefore, that the signals of three satellites would be sufficient to determine a positional fix for our receiver. In theory this is true, but in practice it is not. The reason being that satellite clocks and the receiver clock are never exactly synchronized. Satellite clocks are costly, high-precision, atomic clocks that we can consider synchronized for the time being, but the receiver typically uses a far cheaper, quartz clock that is not synchronized with satellite clocks. This brings an additional unknown variable into play, namely the synchronization bias of the receiver clock, i.e. the difference in time readings between it and the satellite clocks.

Our set of unknown variables has now become (X, Y, Z, Δt) representing a 3D position and a clock bias. The problem can be solved by including the information obtained from a fourth satellite message, (see Figure 2). This will result in the determination of the receiver’s actual position (X, Y, Z), as well as its receiver clock bias Δt, and if we correct the receiver clock for this bias we effectively turn it into a high-precision atomic clock as well!

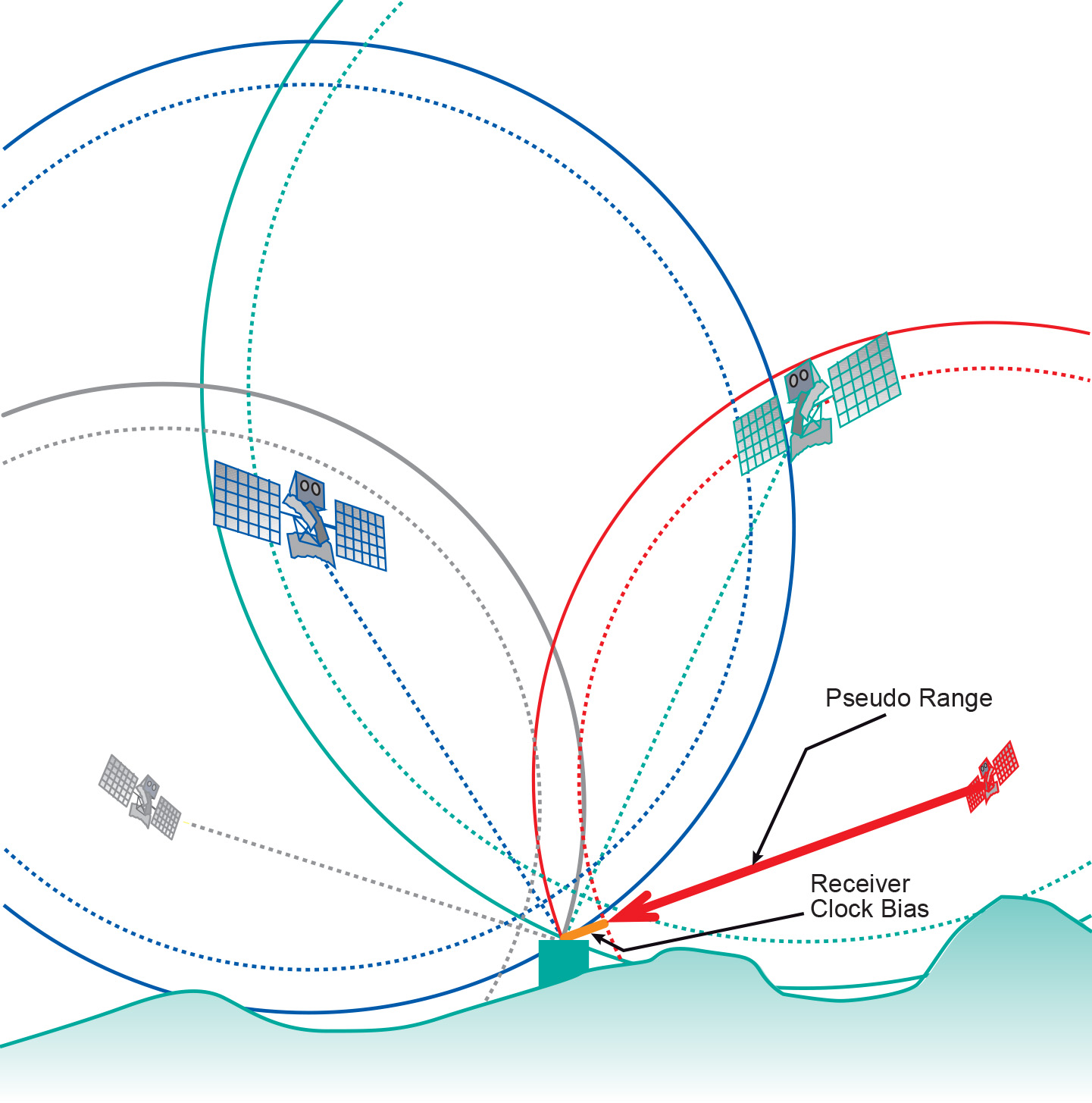
Obtaining a high-precision clock is a fortunate side-effect of using the receiver, as it allows the design of experiments distributed in geographic space that demand high levels of synchronicity. One such application is the use of wireless sensor networks for researching natural phenomena such as earthquakes or meteorological patterns, and for water management.

The positioning of mobile phone users making an emergency call is yet another application. Often callers do not know their location accurately. The telephone company can trace back the call to the receiving transmitter mast, but this may be servicing an area with a radius ranging from 300 m to 6 km. That is far too inaccurate for emergency services. If all masts in the telephony network are equipped with a satellite positioning receiver (and thus, with a very high-precision synchronized clock), however, the time of reception of the call at each mast can be recorded. The time difference of arrival of the call between two nearby masts describes a hyperbola on the ground of possible positions of the caller. If the call is received on three masts, two hyperbolas are described, allowing intersection and thus “hyperbolic positioning”. With current technology the (horizontal) accuracy would be better than 30 m.

Returning to satellite-based positioning, when only three, and not four, satellites are “in view”, the receiver is capable of falling back from the above 3D positioning mode to the inferior 2D positioning mode. With the relative abundance of satellites in orbit around the Earth, this is a relatively rare situation, but it serves to illustrate the importance of 3D positioning.

If a 3D fix had already been obtained, the receiver simply assumes that the height above the ellipsoid has not changed since the last 3D fix. If no fix had been obtained, the receiver assumes that it is positioned at the geocentric ellipsoid adopted by the positioning system, i.e. at height h = 0¹. In the receiver computations, the ellipsoid fills the slot of the missing fourth satellite sphere, and the unknown variables can therefore still be determined. Clearly, in both of these cases, the assumption upon which this computation is based is flawed and the resulting positioning in 2D mode will be unreliable—much more so if no previous fix had been obtained and one’s receiver is not at all near the surface of the geocentric ellipsoid.

References and footnotes:

¹⁾ Any receiver is capable of transforming a coordinate (X, Y, Z), using a straightforward mathematical transformation, into an equivalent coordinate (φ, λ, h), where h is the height above the geocentric ellipsoid.