Network Allocation
Introduction
In network allocation, we have a number of target locations that function as resource centres, and the problem is which part of the network to exclusively assign to which service centre.
This may sound like a simple allocation problem, in which a service centre is assigned those line (segments) to which it is nearest, but usually the problem statement is more complicated. The additional complications stem from the requirements to take into account (a)the capacity with which a centre can produce the resources (whether they are medical operations, seats for school pupils, kilowatts or bottles of milk), and (b) the consumption of the resources, which may vary amongst lines or line segments. After all, some streets have more accidents, more children who live there, more industry in high demand of electricity or just more thirsty workers.
The service area of any centre is a subset of the distribution network, in fact a connected part of the network. Various techniques exist to assign network lines, or their segments, to a centre.
Examples
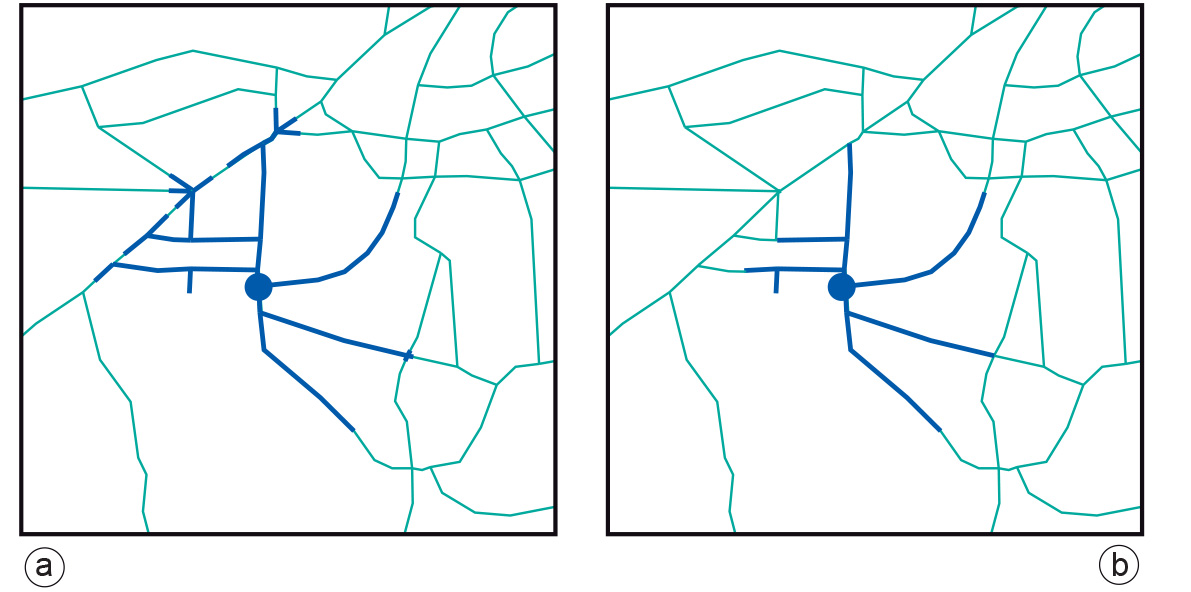
In Figure a, the blue dot indicates a primary school and the GIS has been used to assign streets and street segments along the network within 2 km distance of the school. Then, using demographic figures on pupils living along the streets, it was determined that too many potential pupils lived in the area for the school’s capacity. So in part (b), the part of the network already selected was reduced to match precisely the school’s capacity for pupils in the new school year.
Learning outcomes
-
11 - Spatial analysis: classes of functions
Classify and explain spatial analysis functions (measurements, classification, overlay, neighbourhood and connectivity) in a raster and vector environment (level 1 and 2).
-
12 - Spatial analysis: network analysis
Student is able to explain network analysis and the associated concepts (level 1, 2).
Prior knowledge
Outgoing relations
- Network Allocation is a kind of Network Partitioning