Map projection

A map projection is a mathematically described technique for representing the Earth’s curved surface on a flat map. The actual mapping cannot usually be visualized as a true geometric projection, directly onto the mapping plane. Rather, it is achieved through mapping equations. 

Maps are one of the world’s oldest types of document. In the days that our planet was thought to be flat, a map was simply a miniature representation of a part of the world. To represent the specifically curved Earth’s surface, a map needs to be a flattened representation of a part of the planet. Map projection concerns itself with ways of translating the curved surface of the Earth into a flat, 2D map.

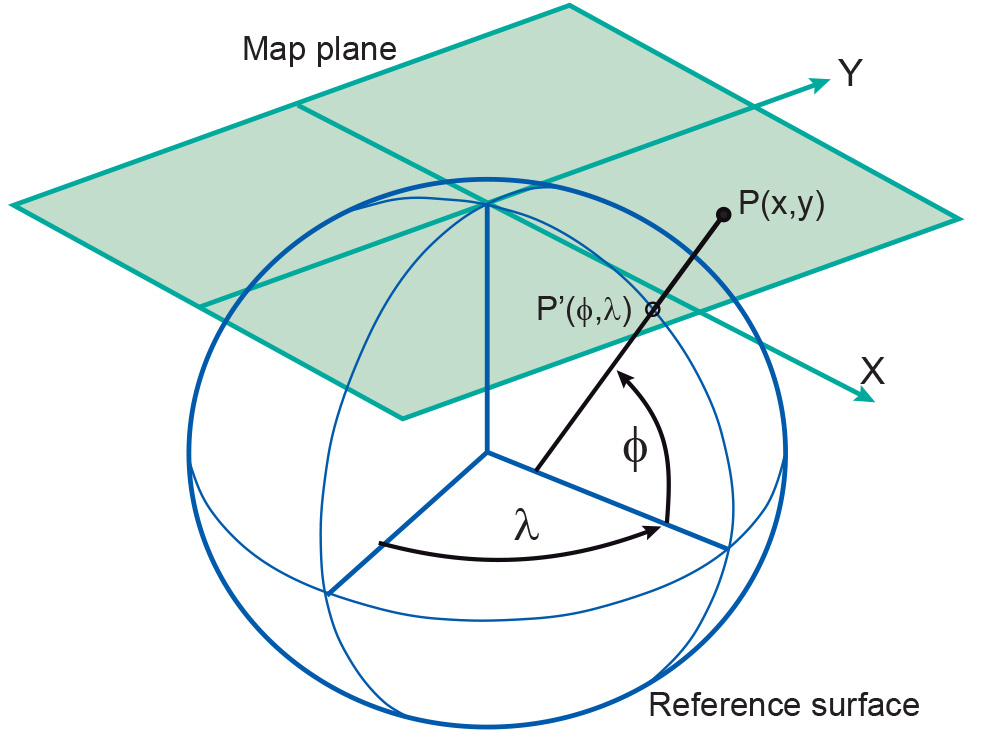
Many map projections have been developed, each with its own specific qualities. More on projection classification in Projection classification.

Choosing a Map Projection

Every map must begin, either consciously or unconsciously, with the choice of a map projection and its parameters. The cartographer's task is to ensure that the right type of projection is used for any particular map. A well-chosen map projection takes care that scale distortions remain within certain limits and that map properties match to the purpose of the map.

Generally, normal cylindrical projections are typically used to map the world in its entirety (in particular areas near the equator are shown well). Conical projections are often used to map the different continents (the mid-latitudes regions are shown well), while the polar azimuthal projections may be used to map the polar areas. Transverse and oblique aspects of many projections can be used for most parts of the world, though they are usually more difficult to construct.

The Universal Transverse Mercator (UTM) is a system of map projection that is used worldwide for large-scale topographic mapping. It is derived from the Transverse Mercator projection (also known as Gauss-Kruger or Gauss conformal projection). UTM uses a transverse cylinder secant to the horizontal reference surface. It divides the world into 60 narrow longitudinal zones of 6 degrees, numbered from 1 to 60. The narrow zones of 6 degrees (and the secant map surface) make the distortions small enough for large-scale mapping.

In theory, the selection of a map projection for a particular area can be made on the basis of:

• the shape of the area

• the location (and orientation) of the area

• the purpose of the map.

Shape

Ideally, the general shape of the mapping area should be well-match with the distortion pattern of a specific projection. If an area is approximately circular, it is possible to create a map that minimizes distortion for that area on the basis of an azimuthal projection. Cylindrical projection is best for a rectangular area and conic projection for a triangular area.

Location and Orientation

The choice of the aspect of a map projection depends largely on the location (and orientation) of the geographic area to be mapped. Optimal is when the projection centre coincides with centre of the area, or when the projection plane is located along the main axis of the area to be mapped.

Distortion and Purpose

The most appropriate type of distortion property for a map depends largely on the purpose for which it will be used. Map projections with a conformal distortion property represent angles and local shapes correctly, but as the region becomes larger, they show considerable area distortions. An example is the Mercator projection. Although Greenland is only one-eighth the size of South America, Greenland appears to be larger.

Maps used for the measurement of angles (e.g. sea, meteorological and aeronautical charts, topographic maps) often make use of a conformal map projection. Map projections with an equal-area distortion property on the other hand, represent areas correctly, but as the region becomes larger, it shows considerable distortions of angles and consequently shapes. Maps which are to be used for measuring areas (e.g. distribution maps and sometimes geological and soil maps) often make use of an equal-area map projection.

The equidistant distortion property is achievable only to a limited degree. That is, true distances can be shown only from one or two points to any other point on the map or in certain directions. If a map is true to scale along the meridians (i.e. no distortion in North-South direction) we say that the map is equidistant along the meridians (e.g. equidistant cylindrical projection in figure). If a map is true to scale along all parallels we say the map is equidistant along the parallels (i.e. no distortion in east-west direction). Maps which require correct distances measured from the centre of the map to any point (e.g. air-route, radio or seismic maps) or maps which require reasonable area and angle distortions (several thematic maps) often make use of an equidistant map projection.