Geographic coordinate system

Geographic (or global) coordinate systems locate data either on the Earth’s surface in a 3D space or on the Earth’s reference surface (ellipsoid or sphere) in a 2D space. This includes: 2D Geographic Coordinates, 3D Geographic Coordinates, and 3D Geocentric Coordinates.

2D geographic coordinates

The most widely used global coordinate system consists of lines of geographic latitude (phi or ϕ or φ) and longitude (lambda or λ) such as 2D Geographic Coordinates. Lines of equal latitude are called parallels. They form circles on the surface of the ellipsoid. Lines of equal longitude are called meridians and form ellipses (meridian ellipses) on the ellipsoid (Figure 1).

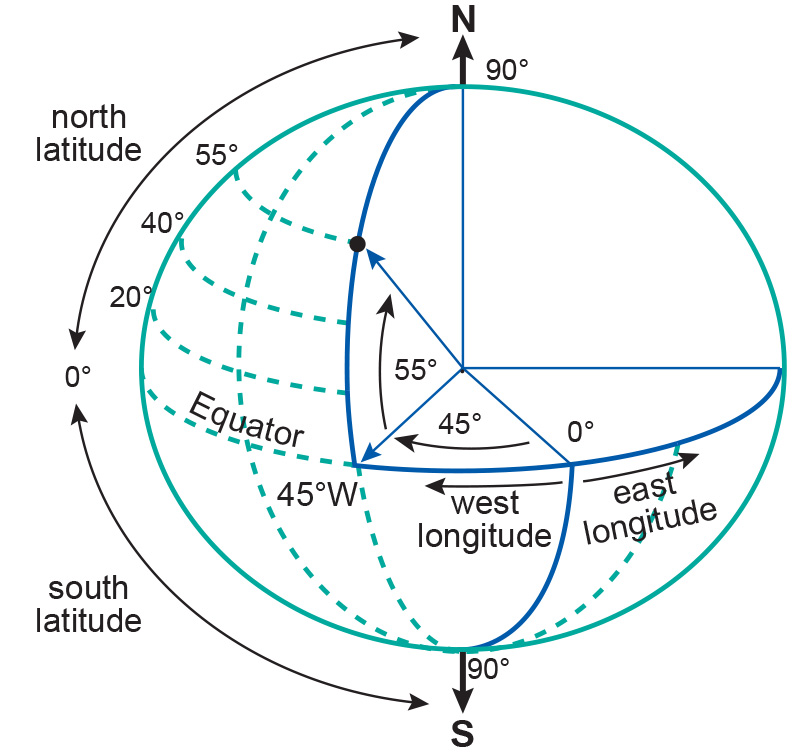
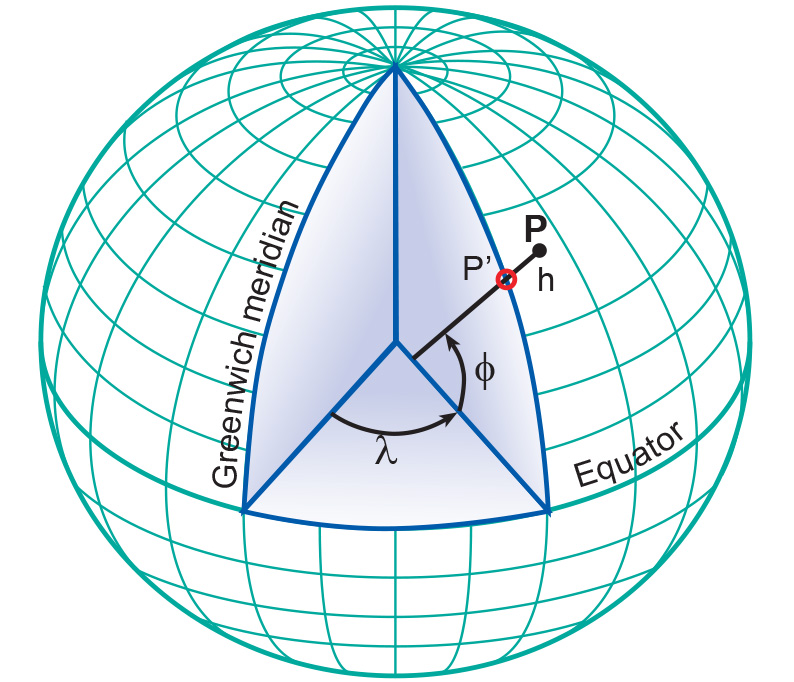
The latitude (ϕ) of a point P (Figure 2) is the angle between the ellipsoidal normal through P’ and the equatorial plane. Latitude is zero on the Equator (ϕ = 0∘), and increases towards the two poles to maximum values of ϕ = +90^∘ (N 90^∘) at the North Pole and ϕ = -90^∘ (S 90^∘) at the South Pole.

The longitude (λ) of the point is the angle between the meridian ellipse that passes through Greenwich and the meridian ellipse containing the point in question. It is measured on the equatorial plane from the meridian of Greenwich (λ = 0^∘), either eastwards through λ = +180^∘ (E 180^∘) or westwards through λ = -180^∘ (W 180^∘).

Latitude and longitude represent the geographic coordinates (ϕ,λ) of a point P’ (Figure 2) with respect to the selected reference surface. They are always given in angular units. For example, the coordinates for the City Hall in Enschede are:

The graticule on a map represents the projected position of the geographic coordinates (ϕ, λ) at constant intervals or, in other words, the projected position of selected meridians and parallels. The shape of the graticule depends largely on the characteristics of the map projection and the scale of the map.

3D Geographic coordinates

3D geographic coordinates (ϕ, λ, h) are obtained by introducing ellipsoidal height (h) into the system. The ellipsoidal height (h) of a point is the vertical distance of the point in question above the ellipsoid. It is measured in distance units along the ellipsoidal normal from the point to the ellipsoid surface. 3D geographic coordinates can be used to define a position on the surface of the Earth (Point P in Figure 2).

Geocentric coordinates

An alternative method for defining a 3D position on the surface of the Earth is to use geocentric coordinates (X, Y, Z), also known as 3D Cartesian coordinates. The system’s origin lies at the Earth’s centre of mass, with the X and Y axes on the plane of the Equator.

The X-axis passes through the meridian of Greenwich and the Z-axis coincides with the Earth’s axis of rotation. The three axes are mutually orthogonal and form a right-handed system. Geocentric coordinates can be used to define a position on the surface of the Earth (point P in Figure 3).

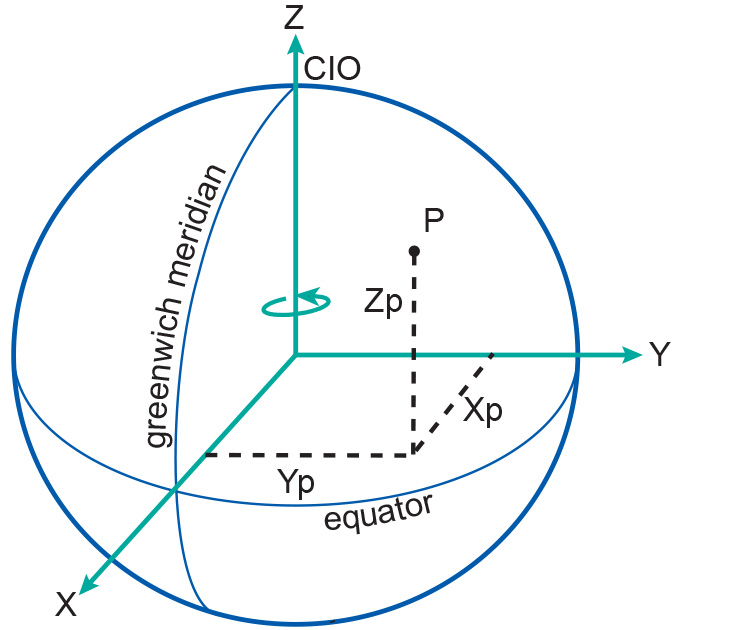
The rotational axis of the Earth, however, changes position over time (referred to as polar motion). To compensate for this, the mean position of the pole in the year 1903 (based on observations between 1900 and 1905) is used to define what is referred to as the “Conventional International Origin” (CIO).