Class separability

Distance and clusters in the feature space

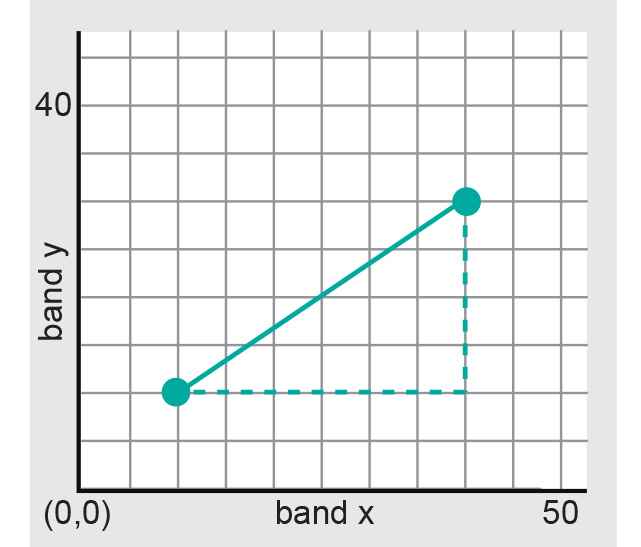
We use distance in the feature space to accomplish classification. Distance in the feature space is measured as Euclidian distance in the same units as the DNs (the unit of the axes). In a two-dimensional feature space, the distance between feature vectors [v₁₁,v₁₂] and [v₂₁,v₂₂] can be calculated according to Pythagoras’ theorem:

For the situation shown in Figure 1, the distance between [10,10] and [40,30] is:

.

For three or more dimensions, the distance is calculated in a similar manner.

Class separability in the feature space

The scatterplot shown above shows the distribution of conjugate pixel values of an actual two-band image. The figure below shows a feature space in which the feature vectors have been plotted of samples of five specific land cover classes (grass, water, trees, etc.). You can see that the feature vectors of GRCs that are water areas form a compact cluster. The feature vectors of the other land cover types (classes) are also clustered. Figure 2 illustrates the basic assumption for image classification: a specific part of the feature space corresponds to a specific class. Once the classes have been defined in the feature space, each feature vector of a multi-band image can be plotted and checked against these classes and assigned to the class where it fits best.

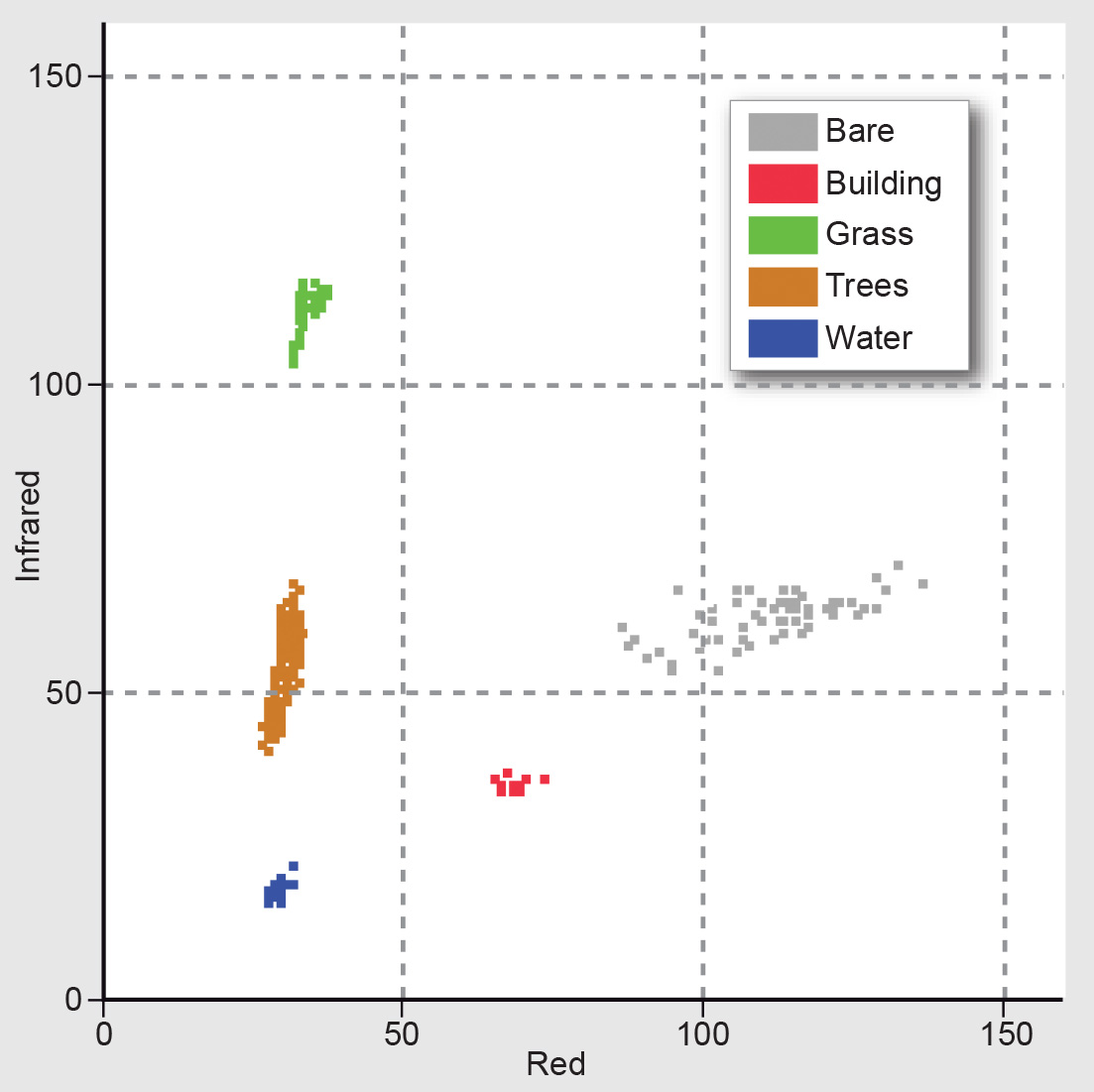
Classes to be distinguished in an image classification need to have different spectral characteristics. This can, for example, be analysed by comparing spectral reflectance curves (Section ??). This brings us to an important limitation of image classification: if classes do not have distinct clusters in the feature space, image classification can only give results to a certain level of reliability.

The principle of image classification is that a pixel is assigned to a class based on its feature vector, by comparing it to predefined clusters in the feature space. Doing so for all pixels results in a classified image. The crux of image classification is in comparing it to predefined clusters, which requires definition of the clusters and methods for comparison. Definition of the clusters is an interactive process and is carried out during the training process. Comparison of the individual pixels with the clusters takes place using classifier algorithms. Both of these concepts are explained in the next subsection.