Planck's law of radiation

Planck’s law of radiation describes the amount of emitted radiation per unit of solid angle in terms of the wavelength and the object’s temperature:

Planck’s law of radiation is only applicable to black bodies.

We can use different measures to quantify radiation. The amount of radiative energy is commonly expressed in joules (J). We may, however, be interested in the radiative energy per unit of time, called the radiant power. We measure the power in watts (W = J s^-1). Radiant emittance is the power emitted from a surface; it is measured in watts per square metre (W m^-2). Spectral radiant emittance characterizes the radiant emittance per wavelength; it is measured in W m^-2 μm^-1 (this is the unit used in Figure 1). Radiance is another quantity frequently used in RS. It is the radiometric quantity that describes the amount of radiative energy being emitted or reflected in a specific direction per unit of projected area per unit of solid angle and per unit of time. Radiance is usually expressed in W sr^-1 m^-2 (sr is steradian, unit of solid angle). Spectral radiance used in Equation 1 is radiance per wavelength and is measured in W sr^-1 m^-2 μm^-1. Irradiance is the amount of incident radiation on a surface per unit of area and per unit of time. Irradiance is usually expressed in W m^-2.

Planck’s law of radiation is illustrated in Figure 1 for the approximate temperature of the Sun (about 6000 K) and the ambient temperature of the Earth’s surface (288 K).

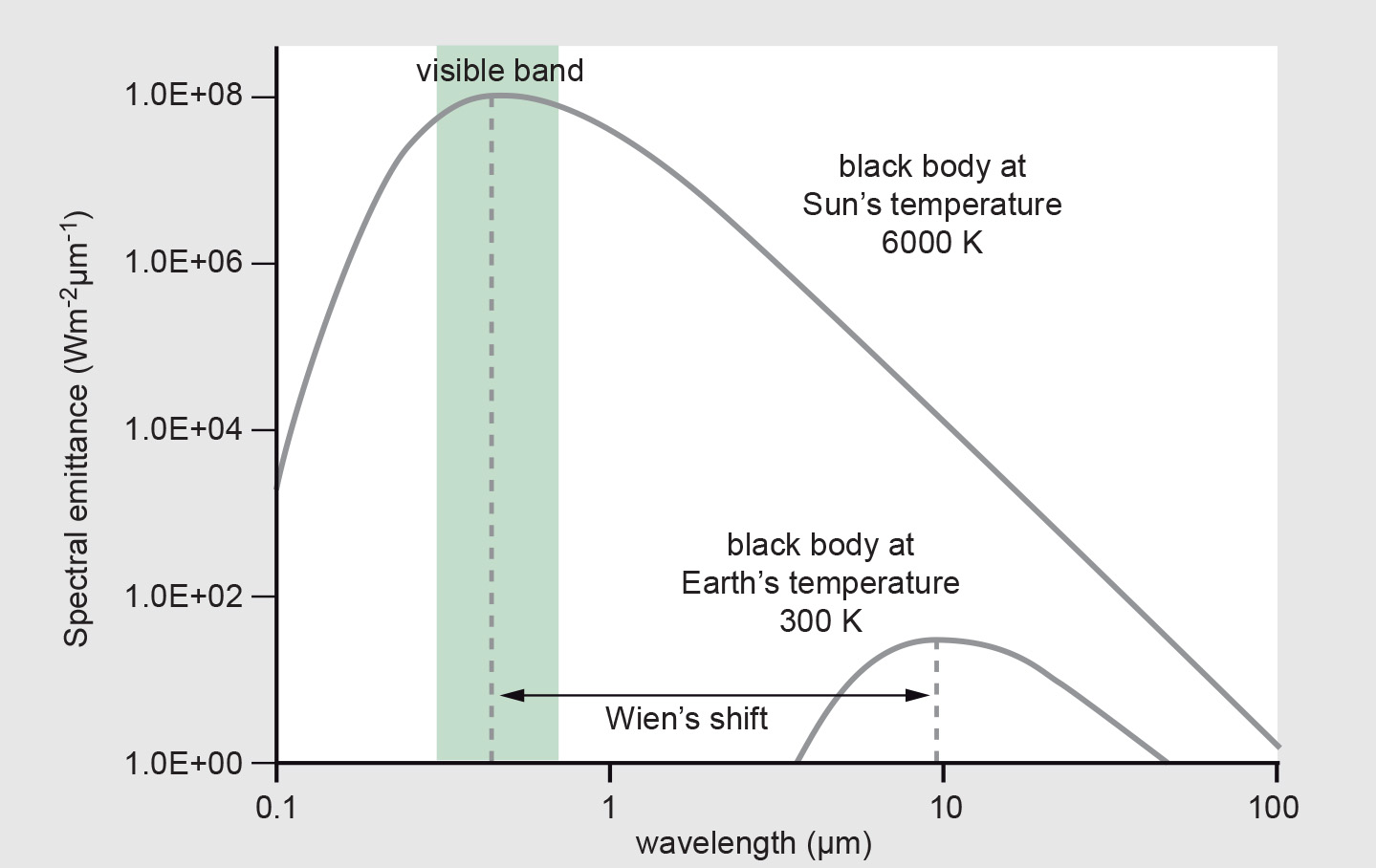
The figure shows that for very hot surfaces (e.g. the Sun), spectral emittance of a black body peaks at short wavelengths. For colder surfaces, such as the Earth, spectral emittance peaks at longer wavelengths. This behaviour is described by Wien’s displacement law:

The following description illustrates the physics of what we see when a blacksmith heats a piece of iron or what we observe when looking at a candle. The flame appears light-blue at the outer edge of its core; there the flame is hottest, with a temperature of 1670 K. The centre, with a temperature of 1070 K, appears orange. More generally, flames may burn with different colours (depending on the material being burnt, the surrounding temperature and the amount of oxygen present) and accordingly have different temperatures (in the range of 600^◦C to 1400^◦C). Colour tells us something about temperature. We can use colour, for example, to estimate the temperature of a lava flow from a safe distance. More generally, if we can build sensors that allow us to detect and quantify EM radiation of different wavelengths (also outside the visible range), we can use RS recordings to estimate the temperature of objects. You may also notice from the black-body radiation curves (Figure 1) that the intensity of EM radiation increases with increasing temperature; the total radiant emittance at a certain temperature is the area under the spectral emittance curve.

If you were interested in monitoring forest fires, which typically burn at 1000 K, you could immediately turn to wavelength bands around 2.9 μm, where the radiation maximum for those fires is to be expected. For ordinary land surface temperatures of around 300 K, wavelengths from 8 to 14 μm are most useful.

You can probably now understand why reflectance remote sensing (i.e. based on reflected
sunlight) uses short wavelengths in the visible and short-wave infrared, and thermal remote sensing (based on emitted Earth radiation) uses the longer wavelengths in the range 3–14 μm. Figure 1 also shows that the total energy (integrated area under the curve) is considerably higher for the Sun than for the cooler Earth’s surface. This relationship between surface temperature and total amount of radiation is described by the Stefan-Boltzmann law.

where M is the total radiant emittance (W m⁻²), σ is the Stefan-Boltzmann constant
(σ ≈ 5.6697 × 10⁻⁸ (W m⁻² K⁻⁴), and T is the temperature in K.

The Stefan-Boltzmann law states that colder objects emit only small amounts of EM radiation. Wien’s displacement law predicts that the peak of the radiation distribution will shift to longer wavelengths as the object gets colder. In Photon model you will have learnt that photons at long wavelengths have less energy than those at short wavelengths. Hence, in thermal RS we are dealing with a small amount of low energy photons, which makes their detection difficult. As a consequence of that, we often have to reduce spatial or spectral resolution when acquiring thermal data, to guarantee an acceptable signal-to-noise ratio.